Hidden Markov modeling for maximum probability neuron reconstruction
- PMID: 35468989
- PMCID: PMC9038756
- DOI: 10.1038/s42003-022-03320-0
Hidden Markov modeling for maximum probability neuron reconstruction
Abstract
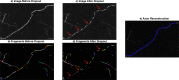
Recent advances in brain clearing and imaging have made it possible to image entire mammalian brains at sub-micron resolution. These images offer the potential to assemble brain-wide atlases of neuron morphology, but manual neuron reconstruction remains a bottleneck. Several automatic reconstruction algorithms exist, but most focus on single neuron images. In this paper, we present a probabilistic reconstruction method, ViterBrain, which combines a hidden Markov state process that encodes neuron geometry with a random field appearance model of neuron fluorescence. ViterBrain utilizes dynamic programming to compute the global maximizer of what we call the most probable neuron path. We applied our algorithm to imperfect image segmentations, and showed that it can follow axons in the presence of noise or nearby neurons. We also provide an interactive framework where users can trace neurons by fixing start and endpoints. ViterBrain is available in our open-source Python package brainlit.
© 2022. The Author(s).
Conflict of interest statement
M.I.M. owns a significant share of Anatomy Works with the arrangement being managed by Johns Hopkins University in accordance with its conflict of interest policies. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Figures


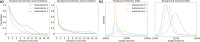




References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

