Direct free energy evaluation of classical and quantum many-body systems via field-theoretic simulation

Abstract

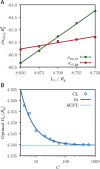
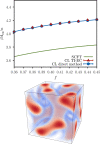
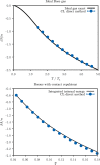
Free energy evaluation in molecular simulations of both classical and quantum systems is computationally intensive and requires sophisticated algorithms. This is because free energy depends on the volume of accessible phase space, a quantity that is inextricably linked to the integration measure in a coordinate representation of a many-body problem. In contrast, the same problem expressed as a field theory (auxiliary field or coherent states) isolates the particle number as a simple parameter in the Hamiltonian or action functional and enables the identification of a chemical potential field operator. We show that this feature leads a “direct” method of free energy evaluation, in which a particle model is converted to a field theory and appropriate field operators are averaged using a field-theoretic simulation conducted with complex Langevin sampling. These averages provide an immediate estimate of the Helmholtz free energy in the canonical ensemble and the entropy in the microcanonical ensemble. The method is illustrated for a classical polymer solution, a block copolymer melt exhibiting liquid crystalline and solid mesophases, and a quantum fluid of interacting bosons.

Keywords: field-theoretic simulation; free energy; molecular simulation; polymers; quantum fluids.

Fig. 1.

Fluctuation contribution to the Helmholtz free energy per chain for the homopolymer solution model as a function of dimensionless chain concentration $C=n{R}_g^3/V$. Three free energy estimation methods were employed based on FTS-CL simulations: the direct method described here, TI of the chemical potential from the ideal gas reference, and TI from an Einstein crystal reference. The solid curve is a Gaussian approximation to the partition function integral that is asymptotic at large C.

Fig. 2.

(A) Example of varying the cell dimension along the interface normal, $L_x=h_{xx}$, of two periods of the lamellar phase of a symmetric diblock copolymer while maintaining the chain concentration and cell dimensions h_yy  =  h_zz in the transverse homogeneous directions constant. Under FTS-CL sampling, the average of the three principal stress components can be brought into agreement, determining the equilibrium cell size. (B) The equilibrium FTS-CL domain spacing, D₀, approaches the SCFT prediction at large dimensionless chain concentrations C. The solid curve is a fit of the form $D_0-D_{0,\text{SCFT}}\sim C^{-1}$ to the simulation data. The lateral cell size is $L_y=L_z=6.0$ R_g for all simulations.

Fig. 3.

(Upper) Free energy comparison between the direct method (blue circles) and TI from an Einstein crystal reference (TI-EC, red triangles) in the equilibrium SCFT cell for a melt of diblock copolymers in the cubic double-gyroid mesophase for various A-block fractions, f. The two methods are in quantitative agreement on the magnitude of fluctuation corrections from the SCFT free energy (green curve). (Lower) A 3D volumetric render of the A domain of the SCFT density for a single conventional cubic cell of the GYR phase at f = 0.36.

Fig. 4.

(Upper) Helmholtz free energy per particle of an ideal gas of bosons as a function of reduced temperature. Direct free energy calculations (blue circles) from CL simulations match the exact ideal gas result of Eq. 16 (black line). The CL simulations used 64 imaginary time samples and 16 spatial samples in each direction; the particle density was fixed at $n/V=2.61$ in units of ${\lambda }_c^{-3}$, where λ_c is the thermal de Broglie wavelength at T_c, and the simulation cell size was set to 2.7 λ_c. (Lower) For bosons with repulsive contact interactions, g  >  0, the Helmholtz free energy per particle computed with the direct method is compared with the internal energy integrated over temperature using Eq. 17. The direct free energy estimate at the lowest temperature is used as a reference to align the integrated energy. The dimensionless particle density is $\overline{\rho }=4.5\times {10}^{-4}$, and the simulation cell size is fixed at 2.65 λ_r. The action (Eq. 7) is discretized with 32 collocation mesh points in each spatial direction and 64 imaginary time slices.