Universality of political corruption networks
- PMID: 35477955
- PMCID: PMC9046414
- DOI: 10.1038/s41598-022-10909-2
Universality of political corruption networks
Abstract
Corruption crimes demand highly coordinated actions among criminal agents to succeed. But research dedicated to corruption networks is still in its infancy and indeed little is known about the properties of these networks. Here we present a comprehensive investigation of corruption networks related to political scandals in Spain and Brazil over nearly three decades. We show that corruption networks of both countries share universal structural and dynamical properties, including similar degree distributions, clustering and assortativity coefficients, modular structure, and a growth process that is marked by the coalescence of network components due to a few recidivist criminals. We propose a simple model that not only reproduces these empirical properties but reveals also that corruption networks operate near a critical recidivism rate below which the network is entirely fragmented and above which it is overly connected. Our research thus indicates that actions focused on decreasing corruption recidivism may substantially mitigate this type of organized crime.
© 2022. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures
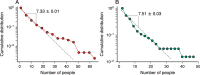
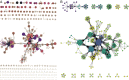

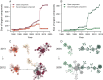
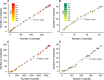

References
-
- Jensen HJ. Self-organized Criticality: Emergent Complex Behavior in Physical and Biological Systems. Cambridge University Press; 1998.
-
- Mitchell M. Complexity: A Guided Tour. Oxford University Press; 2009.
-
- Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009;81:591. doi: 10.1103/RevModPhys.81.591. - DOI
-
- Jusup M, et al. Social physics. Phys. Rep. 2022;948:1–148. doi: 10.1016/j.physrep.2021.10.005. - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

