A robust Bayesian bias-adjusted random effects model for consideration of uncertainty about bias terms in evidence synthesis

Abstract

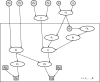
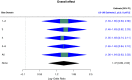
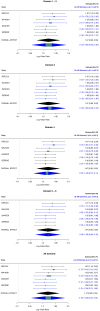
Meta-analysis is a statistical method used in evidence synthesis for combining, analyzing and summarizing studies that have the same target endpoint and aims to derive a pooled quantitative estimate using fixed and random effects models or network models. Differences among included studies depend on variations in target populations (ie, heterogeneity) and variations in study quality due to study design and execution (ie, bias). The risk of bias is usually assessed qualitatively using critical appraisal, and quantitative bias analysis can be used to evaluate the influence of bias on the quantity of interest. We propose a way to consider ignorance or ambiguity in how to quantify bias terms in a bias analysis by characterizing bias with imprecision (as bounds on probability) and use robust Bayesian analysis to estimate the overall effect. Robust Bayesian analysis is here seen as Bayesian updating performed over a set of coherent probability distributions, where the set emerges from a set of bias terms. We show how the set of bias terms can be specified based on judgments on the relative magnitude of biases (ie, low, unclear, and high risk of bias) in one or several domains of the Cochrane's risk of bias table. For illustration, we apply a robust Bayesian bias-adjusted random effects model to an already published meta-analysis on the effect of Rituximab for rheumatoid arthritis from the Cochrane Database of Systematic Reviews.

Keywords: imprecise probability; meta-analysis; risk of bias; robust Bayesian analysis.

FIGURE 1

A probabilistic graphical representation of the Bayesian bias‐adjusted random effects model. Unknown quantities (parameters) are represented by white ellipses, for which priors are specified with fixed hyperparameters (gray circles). Observations (gray squares) are coming from K studies (the plate). The bias terms are fixed and therefore denoted by a gray circle

FIGURE 2

Forestplot of a meta‐analysis of the effectiveness of Rituximab plus metrotexato modified to show bounds on quantities of interest. Unadjusted and robust Bayesian bias‐adjusted random effects log‐odds ratios (with 95% PI) are displayed: (black) unadjusted model; (blue) robust bias‐adjusted random effects model. For the robust bias‐adjusted random effects model, bounds on the expected overall effect, the lower 2.5th percentile and the upper 97.5th percentile are shown

FIGURE 3

Uncertainty in the overall effect per bias domain. For the robust bias‐adjusted random effects model, lower and upper bounds on the expected overall effect, a lower bound on the 2.5th percentile and an upper bound on the 97.5th percentile are shown

FIGURE B1

Forestplot of a meta‐analysis of the effectiveness of Rituximab plus metrotexato modified to show bounds on quantities of interest. Unadjusted and robust Bayesian bias‐adjusted random effects log‐odds ratios (with 95% PI) are displayed: (black) unadjusted model; (blue) robust bias‐adjusted random effects model. For the robust bias‐adjusted random effects model, bounds on the expected overall effect, the lower 2.5th percentile and the upper 97.5th percentile are shown