Meta-analysis of dichotomous and ordinal tests with an imperfect gold standard

Abstract

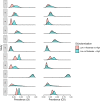
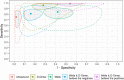
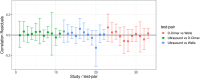
Standard methods for the meta-analysis of medical tests, without assuming a gold standard, are limited to dichotomous data. Multivariate probit models are used to analyse correlated dichotomous data, and can be extended to model ordinal data. Within the context of an imperfect gold standard, they have previously been used for the analysis of dichotomous and ordinal test data from a single study, and for the meta-analysis of dichotomous tests. However, they have not previously been used for the meta-analysis of ordinal tests. In this article, we developed a Bayesian multivariate probit latent class model for the simultaneous meta-analysis of ordinal and dichotomous tests without assuming a gold standard, which also allows one to obtain summary estimates of joint test accuracy. We fitted the models using the software Stan, which uses a state-of-the-art Hamiltonian Monte Carlo algorithm, and we applied the models to a dataset in which studies evaluated the accuracy of tests, and test combinations, for deep vein thrombosis. We demonstrate the issues with dichotomising ordinal test accuracy data in the presence of an imperfect gold standard, before applying and comparing several variations of our proposed model which do not require the data to be dichotomised. The models proposed will allow researchers to more appropriately meta-analyse ordinal and dichotomous tests without a gold standard, potentially leading to less biased estimates of test accuracy. This may lead to a better understanding of which tests, and test combinations, should be used for any given medical condition.

Keywords: imperfect gold; latent class; meta-analysis; multivariate probit; ordinal tests; test accuracy.

FIGURE 1

Posterior medians and 95% posterior intervals for models dichotomising the Well's score. CD, conditional dependence; CI, conditional independence [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 2

Posterior density plots for disease prevalence parameters. CD, conditional dependence; CI, conditional independence [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 3

Posterior medians and 95% posterior intervals for summary sensitivities and specificities, for models 1–4. The Wells score summary estimates are dichotomised as low versus moderate + high. CD, conditional dependence; CI, conditional independence; GS, gold standard [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 4

Posterior medians and 95% posterior intervals for the Well's score stratum, for models 1–4. CD, conditional dependence; CI, conditional independence; GS, gold standard [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 5

Summary receiver operating characteristic (sROC) plot for M4. Shaded regions represent 95% posterior regions and regions surrounded by dashed lines represent 95% prediction regions. The Wells score summary estimates are dichotomised as low versus moderate + high [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 6

Posterior predictive check for model 4; correlation residual plot [Colour figure can be viewed at wileyonlinelibrary.com]