Protein degradation sets the fraction of active ribosomes at vanishing growth

Abstract

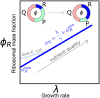
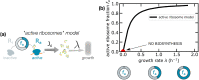
Growing cells adopt common basic strategies to achieve optimal resource allocation under limited resource availability. Our current understanding of such "growth laws" neglects degradation, assuming that it occurs slowly compared to the cell cycle duration. Here we argue that this assumption cannot hold at slow growth, leading to important consequences. We propose a simple framework showing that at slow growth protein degradation is balanced by a fraction of "maintenance" ribosomes. Consequently, active ribosomes do not drop to zero at vanishing growth, but as growth rate diminishes, an increasing fraction of active ribosomes performs maintenance. Through a detailed analysis of compiled data, we show that the predictions of this model agree with data from E. coli and S. cerevisiae. Intriguingly, we also find that protein degradation increases at slow growth, which we interpret as a consequence of active waste management and/or recycling. Our results highlight protein turnover as an underrated factor for our understanding of growth laws across kingdoms.

Fig 1. Sketch of the growth law relating ribosome mass fraction ϕ_R to growth rate λ.

The fraction of ribosomal and ribosome-affiliated proteins (R) increases with increasing nutrient quality at the expense of the sector of metabolic proteins (P), while a fraction of the proteome (Q) is kept to be growth rate-independent. Available data for most organisms show a nonzero intercept ${\varphi }_R^{min}>0$ (see S1 Fig). In E. coli [5], the law deviates from linearity at slow growth (λ ≤ 1 h⁻¹), making the intercept ${\varphi }_R^{min}$ larger.

Fig 2

(a) The standard framework divides ribosomes into two categories—active and inactive—and assumes that only the fraction f_a of active ribosomes is responsible for protein production. (b) The plot reports the estimated values f_a assuming this model and using E. coli data from [5]. The red circle represents the extrapolated point at zero growth.

Fig 3. Protein degradation determines an offset in the first growth law.

(a) Sketch of the first model of protein production proposed in this work, which includes protein degradation but no inactive ribosomes. In this model, ribosomes follow a first-order kinetics to bind the transcripts, and all bound ribosomes contribute to protein synthesis (mass production). Proteins can be lost by protein degradation or diluted by cell growth. (b) The law ϕ_R(λ) predicted by Eq (6) shows an offset ${\varphi }_R^{\text{min}}=\eta /\gamma$. The offset increases linearly with degradation rate η at a constant ribosome production rate γ. (c) Varying γ also changes ${\varphi }_R^{\text{min}}$ but it also affects the slope of ϕ_R(λ). Panel (b) reports ϕ_R(λ) for γ = 7.2 h⁻¹ and η = 0, 0.25, 0.5 h⁻¹. Panel (c) fixes η = 0.25 h⁻¹ and varies γ = 2, 3.6, 7.2 h⁻¹.

Fig 4. Protein degradation increases the fraction of active ribosomes.

(a) Sketch of the second model of protein production proposed in this work, which includes both protein degradation and inactive ribosomes. In this model, only some ribosomes contribute to net protein synthesis. As the model in Fig 3, proteins can be lost by protein degradation or diluted by cell growth. (b) Experimental data on mean degradation rates across conditions for E. coli from [38] and for S. cerevisiae from [42]. The green line is a piece-wise linear fit of the data (see Materials and methods) and the cyan line represents the degradation for the standard model (η = 0). (c) Estimated fraction of active ribosomes in the combined model (turquoise symbols) compared to the model neglecting degradation rates (solid line—lower bound). In absence of degradation, the fraction of active ribosomes is estimated from Eq (1), $f_b=\frac{\lambda }{\gamma {\varphi }_R}$. In presence of degradation, Eq (12) gives $f_b=\frac{\lambda }{\gamma {\varphi }_R}+\frac{\eta }{\gamma {\varphi }_R}$. Turquoise symbols (crosses for E. coli, circles for S. cerevisiae) show the estimates from these formulas for experimental values of the other parameters. The model lower bound (solid line above the shaded area) for the fraction of active ribosomes is the prediction of the active ribosome model, but incorporating the non-null measured degradation rates in these estimates determines considerable deviations from this bound, validating the joint model. Continuous lines are analytical predictions with the constant ratio ansatz, Eq (14). For E. coli, estimates are performed using data for ribosome fractions ϕ_R and translation rate γ from [5] and degradation rates η from [38]. For S. cerevisiae, estimates are performed using data for ribosome fractions and translation rate from [4] and degradation rates from [42].

Fig 5. Maintenance ribosomes are responsible for the increase in active ribosomes in the presence of degradation.

(a) Theoretical curves (in the combined model) of the maintenance ribosome fraction as a function of the degradation rate η for different fixed growth rates λ. Crosses and circles are obtained from experimental data in E. coli and S. cerevisiae respectively. Since f_bm is a function of the ratio η/λ only, the inset shows that such curves collapse if plotted as a function of the degradation-to-growth rate ratio. (b) Maintenance ribosome fraction as a function of growth rate estimated from data, for S. cerevisiae and E. coli. The fraction of maintenance ribosomes is mathematically identical to the relative difference in total active ribosome fraction between the degradation-only model and the standard framework without degradation. Equivalently, the fraction of active ribosome increases in the presence of degradation due to maintenance ribosomes. Degradation data were derived from [38] (E. coli) and [42] (S. cerevisiae). Total ribosome fraction data used in Eq (19) to estimate f_bm come from [5] (E. coli) and [4] (S. cerevisiae).