Chebyshev apodized fiber Bragg gratings

Abstract

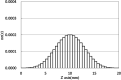
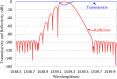
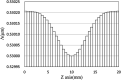
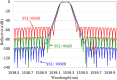
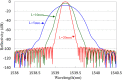
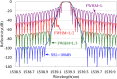
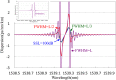
In this paper, a new apodized fiber Bragg grating (FBG) structure, the Chebyshev apodization, is proposed. The Chebyshev polynomial distribution has been widely used for the optimal design of antennas and filters, but it has not been used for designing FBGs. Unlike the function of traditional Gaussian-apodized FBGs, the Chebyshev polynomial is a discrete function. We demonstrate a new methodology for designing Chebyshev-apodized FBGs: the grating region is divided by discrete n sections with uniform gratings, while the index change is used to express the Chebyshev polynomial. We analyze the Chebyshev-apodized FBGs by using coupled mode theory and the piecewise-uniform approach. The reflection spectrum and the dispersion of Chebyshev-apodized FBGs are calculated and compared with those of Gaussian FBGs. Moreover, a sidelobe suppression level (SSL), a parameter of the Chebyshev polynomial, along with the maximum ac-index change of FBGs are analyzed. Assume that the grating length is 20mm, SSL is 100 dB, the section number is 40, and the maximum ac-index change is 2 × 10-4. The reflection spectrum of Chebyshev apodized FBGs shows flattened sidelobes with an absolute SSL of -95.9 dB (corresponding to SSL=100 dB). The simulation results reveal that at the same full width at half maximum, the Chebyshev FBGs have lower sidelobe suppression than the Gaussian FBGs, but their dispersion is similar. We demonstrate the potential of using Chebyshev-apodized FBGs in optical filters, dispersion compensators, and sensors; Chebyshev apodization can be applied in the design of periodic dielectric waveguides.

Keywords: Chebyshev polynomial; Fiber bragg gratings; bragg reflectors; optical fiber devices; optical fiber filters.

Figure 1.

Block diagram for calculating the transmission and reflection efficiencies, group delay, and dispersion of Chebyshev-apodized FBGs.

Figure 2.

dc-index change of a chebyshev profile with 40 section uniform gratings, where $n_1{\sigma }_{dc}(z)$ is a chebyshev function and equals to $n_1{\sigma }_{ac}(z)$ , the gratings length is 20 mm, the length of each section is 0.5 mm, the maximum ac-index change of $n_1{\sigma }_{ac}(z)n_1{\sigma }_{ac\mathrm{\_}max}$ is 2 × 10⁻⁴, and the SSL is 100 dB. The grating period of each section is 0.53μm.

Figure 3.

Transmission and reflection spectra of the chebyshev-apodized structure (parameters presented in Figure 1).

Figure 4.

Index change of a chebyshev profile with 40section uniform gratings and constant dc-index change, where $n_1{\sigma }_{dc}$ is a constant of 2 × 10⁻⁴, $n_1{\sigma }_{ac\mathrm{\_}max}$ is 2 × 10⁻⁴, and the SSL is 100 dB.

Figure 5.

The grating period of each section of chebyshev-apodized structure with grating period variation. The parameters correspond to those in Figure 1, which are calculated using Eq. (9). The total number of sections is 40. The grating period at the 20th and 21st sections is 0.53μm.

Figure 6.

Transmission and reflection spectra of a chebyshev-apodized FBGs with zero dc-index change and grating period variation under the same parameters as shown in Figure 3 and Figure 4. Note that spectra of zero dc-index change and grating period variation are the same.

Figure 7.

The reflection spectrum of chebyshev-apodized structure with SSL = 60 dB (red line), SSL = 80 dB (green line) and SSL = 100 dB (blue line), where SN = 40, and $n_1{\sigma }_{dc}=n_1{\sigma }_{ac\mathrm{\_}max}$   = 2 × 10⁻⁴. The grating period is 0.53 μm.

Figure 8.

Reflection spectrum of a chebyshev-apodized structure with $n_1{\sigma }_{dc}=n_1{\sigma }_{ac\mathrm{\_}max}$    = 2 × 10⁻⁵ (red line), 2 × 10⁻⁴ (blue line), and 7 × 10⁻⁴ (green line). The SSL is 80 dB, and SN is 40.

Figure 9.

Reflection spectrum of a chebyshev-apodized structure with the gratings length of 20 mm, 10 mm, and 5 mm. The $n_1{\sigma }_{dc}=n_1{\sigma }_{ac\mathrm{\_}max}$   = 2 × 10⁻⁴, SSL is 100 dB, and SN is 40.

Figure 10.

Reflection spectra of chebyshev-apodized (blue line for an SSL of 100 dB) and Gaussian-apodized FBGs (green line for FWHM = 7 mm ≈ L/3, red line for FWHM = 10 mm = L/2, and purple line for FWHM = 20 mm = L).

Figure 11.

Dispersion spectra of the chebyshev-apodized (blue line) and Gaussian-apodized FBGs. The green line represents FWHM = 7 mm, the red line denotes FWHM = 10 mm, and the purple line denotes FWHM = 20 mm. The insect is the dispersion spectrum of FWHM = 10 mm.