Functional group bridge for simultaneous regression and support estimation

Abstract

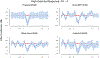
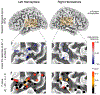
This paper is motivated by studying differential brain activities to multiple experimental condition presentations in intracranial electroencephalography (iEEG) experiments. Contrasting effects of experimental conditions are often zero in most regions and nonzero in some local regions, yielding locally sparse functions. Such studies are essentially a function-on-scalar regression problem, with interest being focused not only on estimating nonparametric functions but also on recovering the function supports. We propose a weighted group bridge approach for simultaneous function estimation and support recovery in function-on-scalar mixed effect models, while accounting for heterogeneity present in functional data. We use B-splines to transform sparsity of functions to its sparse vector counterpart of increasing dimension, and propose a fast nonconvex optimization algorithm using nested alternative direction method of multipliers (ADMM) for estimation. Large sample properties are established. In particular, we show that the estimated coefficient functions are rate optimal in the minimax sense under the L₂ norm and resemble a phase transition phenomenon. For support estimation, we derive a convergence rate under the $L_{\infty }$ norm that leads to a selection consistency property under δ-sparsity, and obtain a result under strict sparsity using a simple sufficient regularity condition. An adjusted extended Bayesian information criterion is proposed for parameter tuning. The developed method is illustrated through simulations and an application to a novel iEEG data set to study multisensory integration.

Keywords: function-on-scalar regression; iEEG; locally sparse function; minimax rate; nonconvex optimization; selection consistency.

Figure 1.

Baseline corrected response of iEEG high-gamma power under auditory-only (left) and audiovisual (right) conditions on one selected electrode. The data are obtained by decomposing the measured voltage signal into frequency space, converting to Decibel unit, calibrated to baseline (from −1 to −0.3 seconds), and then taking the average power in the 70–150Hz range. Each individual grey line is one trial. The bold solid line is the mean responses, and the shaded area around the mean is a pointwise 95% confidence interval. This figure appears in color in the electronic version of this article, and any mention of color refers to that version.

Figure 2.

Fitted coefficients with 95% joint confidence intervals at n = 100 (top two rows) and n = 1000 (bottom two rows). This figure appears in color in the electronic version of this article, and any mention of color refers to that version.

Figure 3.

ROC curve for each method with n = 100 (left) and n = 1000 (right), averaged over 100 simulations. This figure appears in color in the electronic version of this article, and any mention of color refers to that version.

Figure 4.

Effect of AV versus A estimated by various methods using the data in Figure 1. In each plot, the solid line (blue) is the estimated effect ${\widehat{\beta }}_2(t)$, shaded area (light-blue) is the joint 95% confidence band, and dashed line (grey) is the estimated effect from ordinary least squares at each time point. This figure appears in color in the electronic version of this article, and any mention of color refers to that version.

Figure 5.

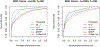
First row: visualization of all 65 electrodes mapped onto N27 template brain. Second row: lower 5% quantile value of AV-A from auditory onset to 500 ms after the auditory onset. Color coding: blue for suppression introduced by visual stimuli, gray for little to no differences, and red for that AV is greater than A. Third row: p-values for each electrodes with alternative hypothesis of AV less than A response. This figure appears in color in the electronic version of this article, and any mention of color refers to that version.