Bond orders of the diatomic molecules

Abstract

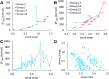
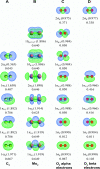
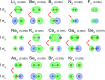
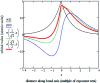
Bond order quantifies the number of electrons dressed-exchanged between two atoms in a material and is important for understanding many chemical properties. Diatomic molecules are the smallest molecules possessing chemical bonds and play key roles in atmospheric chemistry, biochemistry, lab chemistry, and chemical manufacturing. Here we quantum-mechanically calculate bond orders for 288 diatomic molecules and ions. For homodiatomics, we show bond orders correlate to bond energies for elements within the same chemical group. We quantify and discuss how semicore electrons weaken bond orders for elements having diffuse semicore electrons. Lots of chemistry is effected by this. We introduce a first-principles method to represent orbital-independent bond order as a sum of orbital-dependent bond order components. This bond order component analysis (BOCA) applies to any spin-orbitals that are unitary transformations of the natural spin-orbitals, with or without periodic boundary conditions, and to non-magnetic and (collinear or non-collinear) magnetic materials. We use this BOCA to study all period 2 homodiatomics plus Mo₂, Cr₂, ClO, ClO^-, and Mo₂(acetate)₄. Using Manz's bond order equation with DDEC6 partitioning, the Mo-Mo bond order was 4.12 in Mo₂ and 1.46 in Mo₂(acetate)₄ with a sum of bond orders for each Mo atom of ∼4. Our study informs both chemistry research and education. As a learning aid, we introduce an analogy between bond orders in materials and message transmission in computer networks. We also introduce the first working quantitative heuristic model for all period 2 homodiatomic bond orders. This heuristic model incorporates s-p mixing to give heuristic bond orders of ¾ (Be₂), 1¾ (B₂), 2¾ (C₂), and whole number bond orders for the remaining period 2 homodiatomics.

Fig. 1. (A) and (B) Bond order versus bond energy for homodiatomics of each main group; (C) bond order versus bond energy for all homodiatomics studied; (D) bond order versus atomic charge magnitude for all heterodiatomics studied. These plots do not include any diatomic ions.

Fig. 2. Bond order component analysis (BOCA) for C₂ (singlet), Mo₂ (singlet), and O₂ (triplet) molecules using the natural spin-orbitals. Orbital occupancies are given in parentheses. Bond order components are listed without parentheses.

Fig. 3. Graphic showing diffuse semicore electrons decrease the bond order. (A) Plot of core electron density versus distance along the C–C axis in C₂. The red, brown, and green lines demarcate the 10⁻¹, 10⁻², and 10⁻³ e bohr⁻³ electron density thresholds corresponding to the distances d₋₁, d₋₂, and d₋₃, respectively. (B) Formula used to compute the percentage of the bond length for which the (semi-)core electron density is above each threshold (aka ‘(semi-)core percentages’). (C) Partial periodic table (periods 2–5 and groups 1–2, 13–17) showing trends in the bond orders (black) and (semi-)core percentages corresponding to the respective density thresholds (red, brown, and green).

Fig. 4. 1σ_g and 1σ_u NSOs for high-level quantum chemistry calculations of period 2 and 4 main-group homodiatomics. (The C₂ and O₂ orbitals are shown in Fig. 2.) The arrows indicate orbitals showing strong s–p mixing. S–p mixing is visible in a 1σ_g orbital as pockets intruding into the two ends of the orbital. S–p mixing is visible in the 1σ_u orbital as pockets intruding into the lobe centers. Numbers in parentheses are the orbital contour values in atomic units. For each molecule, the contour value was chosen to maximize visual clarity.

Fig. 5. Plot of s-orbital (black), p-orbital (blue), and two s–p hybrids along the z-axis of a single atom. A s–p hybrid with equal coefficients of s and p orbitals is shown in green. The s–p hybrid (red) with (√3s^A + p_z^A)/2 is approximately optimal, because it has a value of zero at zζ = −1.

Fig. 6. Bond order component analysis for Mo₂(acetate)₄ using the Pipek–Mezey localized orbitals of the B3LYP/def2tzvppd electron density matrix. The corresponding bond order component per orbital is listed. For each orbital, the total number of analogous orbitals is shown in parentheses. For each displayed Mo–O bonding orbital, the eight analogous orbitals correspond to one per oxygen atom. There are four Mo–Mo bonding orbitals. The two 1π_u orbitals (top right panel) are rotated 90° relative to each other. The right column lists computed partial atomic charges, SBOs, and selected bond orders.

Fig. 7. Bond order component analysis (BOCA) for the ClO (doublet) molecule and ClO⁻ (singlet) anion using the natural spin-orbitals. Orbital occupancies are given in parentheses. Bond order components are listed without parentheses. The oxygen atom is displayed in red, while the chlorine atom is displayed in green.

Fig. 8. Histogram for the bond length error. This plot includes all the homodiatomics and heterodiatomics for which reference experimental bond lengths are listed.