Frequency-dependent transition in power-law rheological behavior of living cells

Abstract

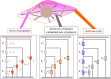
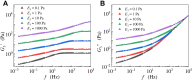
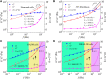
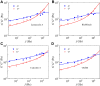
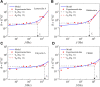
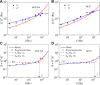
Living cells are active viscoelastic materials exhibiting diverse mechanical behaviors at different time scales. However, dynamical rheological characteristics of cells in frequency range spanning many orders of magnitude, especially in high frequencies, remain poorly understood. Here, we show that a self-similar hierarchical model can capture cell's power-law rheological characteristics in different frequency scales. In low-frequency scales, the storage and loss moduli exhibit a weak power-law dependence on frequency with same exponent. In high-frequency scales, the storage modulus becomes a constant, while the loss modulus shows a power-law dependence on frequency with an exponent of 1.0. The transition between low- and high-frequency scales is defined by a transition frequency based on cell's mechanical parameters. The cytoskeletal differences of different cell types or states can be characterized by changes in mechanical parameters in the model. This study provides valuable insights into potentially using mechanics-based markers for cell classification and cancer diagnosis.

Fig. 1.. The self-similar hierarchical model of cells.

The 1st-level hierarchy is constructed as a ladder-like structure where springs with stiffness E₁ run along the struts and dashpots with viscosity η on the rungs of the ladder (elements are numbered in red). The 2nd-level hierarchy is constructed by having the 1st-level hierarchy as building block G₁ along with springs of stiffness E₂. The 3rd-level hierarchy is constructed by arranging the 2nd-level hierarchy as building block G₂ along with springs of stiffness E₃. In this model, the cytoplasm serves as the 1st-level hierarchy that fills the entire cell; the cytoskeletal filament (e.g., microtubule) embedded into the cytoplasm is considered the 2nd-level hierarchy; and lastly, the entire cell is modeled as the 3rd-level hierarchy.

Fig. 2.. Comparison between analytical (Eq. 4) and numerical solutions.

The solid lines and scatter points represent analytical and numerical results, respectively. The (A) storage and (B) loss moduli of the 3rd-level hierarchy versus angular frequency for different values of E₃.

Fig. 3.. Cells exhibit different rheological behavior at different frequency scales.

Our proposed self-similar hierarchical model can realize the rheological characteristics of different types of cells in different frequency ranges. Both storage and loss moduli of (A) neuronal cells (12) and (B) 3T3 fibroblasts (10) are consistent with our models. The predictions of our model (solid line) fit well with experimental data of (C) HASM cells (9) and (D) bronchial (BEAS-2B) epithelial cells (25) in a vast frequency range. Depending on the loss tangent δ, the complex moduli of cells can be divided into three regions, indicated by green (region I), yellow (region II), and purple (region III), respectively.

Fig. 4.. The predictions of our self-similar hierarchical model are in agreement with the experimental data (10) of 3T3 fibroblast cells treated with different drugs.

Frequency-dependent storage and loss moduli of cells treated with the drug (A) latrunculin A, (B) blebbistatin, (C) calyculin A, and (D) CK666. The obtained mechanical parameters are in accord with drug-induced biological changes, as shown in Table 1.

Fig. 5.. The transition frequency of cells treated with different drugs.

(A) Latrunculin A, (B) blebbistatin, (C) calyculin A, and (D) CK666. Experimental data are obtained from (10).

Fig. 6.. The self-similar hierarchical model agrees well with experimental results from (10).

Frequency-dependent storage and loss moduli of (A) MCF10A and (B) MCF7 cancer cells. Frequency-dependent loss tangents δ of (C) benign MCF10A and (D) malignant MCF7 cancer cells.