Neurite Exchange Imaging (NEXI): A minimal model of diffusion in gray matter with inter-compartment water exchange
- PMID: 35523369
- PMCID: PMC10363376
- DOI: 10.1016/j.neuroimage.2022.119277
Neurite Exchange Imaging (NEXI): A minimal model of diffusion in gray matter with inter-compartment water exchange
Abstract
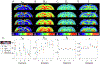
Biophysical models of diffusion in white matter have been center-stage over the past two decades and are essentially based on what is now commonly referred to as the "Standard Model" (SM) of non-exchanging anisotropic compartments with Gaussian diffusion. In this work, we focus on diffusion MRI in gray matter, which requires rethinking basic microstructure modeling blocks. In particular, at least three contributions beyond the SM need to be considered for gray matter: water exchange across the cell membrane - between neurites and the extracellular space; non-Gaussian diffusion along neuronal and glial processes - resulting from structural disorder; and signal contribution from soma. For the first contribution, we propose Neurite Exchange Imaging (NEXI) as an extension of the SM of diffusion, which builds on the anisotropic Kärger model of two exchanging compartments. Using datasets acquired at multiple diffusion weightings (b) and diffusion times (t) in the rat brain in vivo, we investigate the suitability of NEXI to describe the diffusion signal in the gray matter, compared to the other two possible contributions. Our results for the diffusion time window 20-45 ms show minimal diffusivity time-dependence and more pronounced kurtosis decay with time, which is well fit by the exchange model. Moreover, we observe lower signal for longer diffusion times at high b. In light of these observations, we identify exchange as the mechanism that best explains these signal signatures in both low-b and high-b regime, and thereby propose NEXI as the minimal model for gray matter microstructure mapping. We finally highlight multi-b multi-t acquisition protocols as being best suited to estimate NEXI model parameters reliably. Using this approach, we estimate the inter-compartment water exchange time to be 15 - 60 ms in the rat cortex and hippocampus in vivo, which is of the same order or shorter than the diffusion time in typical diffusion MRI acquisitions. This suggests water exchange as an essential component for interpreting diffusion MRI measurements in gray matter.
Keywords: Cell membrane permeability; Cortex; Diffusion MRI; Exchange; Gray matter; Microstructure.
Copyright © 2022. Published by Elsevier Inc.
Conflict of interest statement
Declaration of Competing Interest None.
Figures

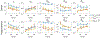
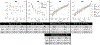
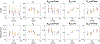
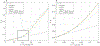
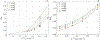
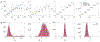

Similar articles
-
Diffusion time dependence, power-law scaling, and exchange in gray matter.Neuroimage. 2022 May 1;251:118976. doi: 10.1016/j.neuroimage.2022.118976. Epub 2022 Feb 7. Neuroimage. 2022. PMID: 35168088 Free PMC article.
-
Quantifying human gray matter microstructure using neurite exchange imaging (NEXI) and 300 mT/m gradients.Imaging Neurosci (Camb). 2024 Mar 6;2:imag-2-00104. doi: 10.1162/imag_a_00104. eCollection 2024. Imaging Neurosci (Camb). 2024. PMID: 40800458 Free PMC article.
-
Compartmental diffusion and microstructural properties of human brain gray and white matter studied with double diffusion encoding magnetic resonance spectroscopy of metabolites and water.Neuroimage. 2021 Jul 1;234:117981. doi: 10.1016/j.neuroimage.2021.117981. Epub 2021 Mar 21. Neuroimage. 2021. PMID: 33757904 Free PMC article.
-
Probing brain tissue microstructure with MRI: principles, challenges, and the role of multidimensional diffusion-relaxation encoding.Neuroimage. 2023 Nov 15;282:120338. doi: 10.1016/j.neuroimage.2023.120338. Epub 2023 Aug 19. Neuroimage. 2023. PMID: 37598814 Review.
-
In Vivo Imaging of Gray Matter Microstructure in Major Psychiatric Disorders: Opportunities for Clinical Translation.Biol Psychiatry Cogn Neurosci Neuroimaging. 2020 Sep;5(9):855-864. doi: 10.1016/j.bpsc.2020.03.003. Epub 2020 Mar 25. Biol Psychiatry Cogn Neurosci Neuroimaging. 2020. PMID: 32381477 Review.
Cited by
-
Gradual changes in microarchitectural properties of cortex and juxtacortical white matter: Observed by anatomical and diffusion MRI.Magn Reson Med. 2022 Dec;88(6):2485-2503. doi: 10.1002/mrm.29413. Epub 2022 Aug 31. Magn Reson Med. 2022. PMID: 36045582 Free PMC article.
-
Cerebral microstructural alterations in Post-COVID-condition are related to cognitive impairment, olfactory dysfunction and fatigue.Nat Commun. 2024 May 18;15(1):4256. doi: 10.1038/s41467-024-48651-0. Nat Commun. 2024. PMID: 38762609 Free PMC article.
-
Diffusion Tensor Imaging in Neurofluids.Neuroimaging Clin N Am. 2025 May;35(2):211-222. doi: 10.1016/j.nic.2024.11.001. Epub 2025 Feb 21. Neuroimaging Clin N Am. 2025. PMID: 40210378 Review.
-
3D MERMAID: 3D Multi-shot enhanced recovery motion artifact insensitive diffusion for submillimeter, multi-shell, and SNR-efficient diffusion imaging.Magn Reson Med. 2025 Jun;93(6):2311-2330. doi: 10.1002/mrm.30436. Epub 2025 Mar 4. Magn Reson Med. 2025. PMID: 40035173 Free PMC article.
-
Disentangling the effects of restriction and exchange with diffusion exchange spectroscopy.Front Phys. 2022;10:805793. doi: 10.3389/fphy.2022.805793. Epub 2022 Mar 23. Front Phys. 2022. PMID: 37063496 Free PMC article.
References
-
- Andersson M, Kjer HM, Rafael-Patino J, Pacureanu A, Pakkenberg B, Thiran JP, Ptito M, Bech M, Dahl AB, Dahl VA, Dyrby TB, 2020. Axon morphology is modulated by the local environment and impacts the noninvasive investigation of its structure–function relationship. PNAS 117, 33649–33659. doi: 10.1073/pnas.2012533117. - DOI - PMC - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

