Different directional energy dissipation of heterogeneous polymers in bimodal atomic force microscopy

Abstract

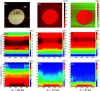
Dynamic force microscopy (DFM) has become a multifunctional and powerful technique for the study of the micro-nanoscale imaging and force detection, especially in the compositional and nanomechanical properties of polymers. The energy dissipation between the tip and sample is a hot topic in current materials science research. The out-of-plane interaction can be measured by the most commonly used tapping mode DFM, which exploits the flexural eigenmodes of the cantilever and a sharp tip vibrating perpendicular to the sample surface. However, the in-plane interaction cannot be detected by the tapping mode. Here a bimodal approach, where the first order flexural and torsional eigenmodes of the cantilever are simultaneously excited, was developed to detect the out-of-plane and in-plane dissipation between the tip and the polymer blend of polystyrene (PS) and low-density polyethylene (LDPE). The vibration amplitudes and phases have been recorded to obtain the contrast, energy dissipation and virial versus the setpoint ratio of the first order vibration amplitude. The pull-in phenomenon caused by a strong attractive force can occur near the transitional setpoint ratio value, the amplitude setpoint at which the mean force changes from overall attractive to overall repulsive. The in-plane dissipation is much lower than out-of-plane dissipation, but the torsional amplitude image contrast is higher when the tip vibrates near the sample surface. The average tip-sample distance can be controlled by the setpoint ratio to study the in-plane dissipation. Both flexural and torsional phase contrasts and torsional amplitude contrast can also be significantly enhanced in the intermediate setpoint ratio range, in which compliant heterogeneous materials can be distinguished. The experiment results are of great importance to optimize the operating parameters of image contrast and reveal the mechanism of friction dissipation from the perspective of in- and out-of-plane energy dissipation at different height levels, which adds valuable ideas for the future applications, such as compliant materials detection, energy dissipation and the lateral micro-friction measurement and so on.

Fig. 1. Bimodal schematic description and control system. The two excitation frequencies are the first order flexural and torsional mode frequencies, respectively. The response of the cantilever contains two frequency components same as the excitation frequencies. The flexural signal is used for topography feedback and the flexural dissipation, while the torsional signal is utilized to detect the torsional dissipation.

Fig. 2. The frequency spectra (200–2500 kHz) of the cantilever PPP-NCH. (a) The flexural signal spectral response (red line) and the first order flexural vibration frequency f₁ = 288.3 kHz. (b) The torsional signal spectral response (blue line) and the first order torsional vibration frequency f_tr = 2326.9 kHz. The inset is the details of the first order torsional resonance peak in the red box. The unit nA is an electric parameter in the AFM apparatus representing the amplitude response of the cantilever.

Fig. 3. 4.5 × 4.5 micrometer AFM signals of PS–LDPE imaged by an Nanosensors PPP-NCH cantilever in the bimodal AFM mode. Free amplitudes (a) A₀₁ = 254 nm, (b) A₀₁ = 123 nm and (c) A₀₁ = 65 nm. The left value is the setpoint ratio. (i) Setpoint = 0.735, (ii) transitional setpoint, and (iii) setpoint = 0.074 in (a), 0.05 in (b) and (c) are the three chosen values of the setpoint ratio performed at the respective A₀₁. The amplitude and phase images are in nm and degrees, respectively.

Fig. 4. The phase, energy dissipation power and virial of the first order flexural and torsional signals under different free flexural A₀₁ with the various setpoint ratio (0–1). The setpoint ratio axis is divided into two regions I and II in (a), (b), (d) and (f). (a) The first order flexural vibration phase φ₁. (b) The first order torsional vibration phase φ_tr. (c) Energy dissipation power of the first order flexural vibration mode. (d) Energy dissipation power of the first order torsional vibration mode. (e) Virial of the first order flexural vibration mode. (f) Virial of the first order torsional vibration mode. The first order free flexural vibration amplitude A₀₁ is 254 nm (red line), 123 nm (blue line) and 65 nm (green line). The square dots and open circle dots represent the data on the PS and LDPE, respectively. The data points are the comprehensive reflection of the scanning image pixels by fitting the normal distribution. They are the data after error processing. The errors involved are less than the symbol size in all plots, but the data points are very close within the small setpoint ratio range, in which the experiment should be avoided because of the possible tip contamination.

Fig. 5. The sectional energy dissipation distribution. (a) Phase image of the PS/LDPE. (b) Cross sectional flexural dissipation distribution at the setpoint amplitude 54 nm (A₀₁ = 123 nm) as shown by the black line in (e). (c) Cross sectional torsional dissipation distribution at the setpoint amplitude 6.5 nm (A₀₁ = 65 nm) as shown by the green line in (i). The longitudinal sectional flexural dissipation distribution at (d) A₀₁ = 254 nm (e) A₀₁ = 123 nm and (f) A₀₁ = 65 nm. The longitudinal sectional torsional dissipation distribution at (g) A₀₁ = 254 nm (h) A₀₁ = 123 nm and (i) A₀₁ = 65 nm. The side length is 4.5 micrometer and the longitudinal sectional position of (d)–(i) is the yellow line in (a).

Fig. 6. The amplitude and phase contrast of the first order flexural and torsional signals under different free flexural A₀₁ in the various setpoint ratio range. The setpoint ratio axis is divided into three regions I, II and III in every image set. (a) The first order flexural vibration phase φ₁ contrast. (b) The first order torsional vibration amplitude A_tr. (c) The first order torsional vibration phase φ_tr contrast. (d) The first order torsional vibration amplitude A_tr contrast. The purple dotted lines are the boundaries between different contrast stage. The first order free flexural vibration amplitude A₀₁ is 254 nm (red line), 123 nm (blue line) and 65 nm (green line).