Parameter estimation of the COVID-19 transmission model using an improved quantum-behaved particle swarm optimization algorithm
- PMID: 35529477
- PMCID: PMC9067002
- DOI: 10.1016/j.dsp.2022.103577
Parameter estimation of the COVID-19 transmission model using an improved quantum-behaved particle swarm optimization algorithm
Abstract
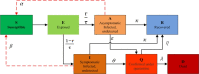
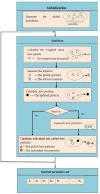
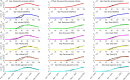
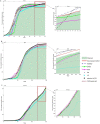
The outbreak of coronavirus disease (COVID-19) and its accompanying pandemic have created an unprecedented challenge worldwide. Parametric modeling and analyses of the COVID-19 play a critical role in providing vital information about the character and relevant guidance for controlling the pandemic. However, the epidemiological utility of the results obtained from the COVID-19 transmission model largely depends on accurately identifying parameters. This paper extends the susceptible-exposed-infectious-recovered (SEIR) model and proposes an improved quantum-behaved particle swarm optimization (QPSO) algorithm to estimate its parameters. A new strategy is developed to update the weighting factor of the mean best position by the reciprocal of multiplying the fitness of each best particle with the average fitness of all best particles, which can enhance the global search capacity. To increase the particle diversity, a probability function is designed to generate new particles in the updating iteration. When compared to the state-of-the-art estimation algorithms on the epidemic datasets of China, Italy and the US, the proposed method achieves good accuracy and convergence at a comparable computational complexity. The developed framework would be beneficial for experts to understand the characteristics of epidemic development and formulate epidemic prevention and control measures.
Keywords: COVID-19; Mathematical modeling; Parameter estimation; Quantum-behaved particle swarm optimization.
© 2022 Elsevier Inc. All rights reserved.
Conflict of interest statement
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures




Similar articles
-
An Improved Quantum-Behaved Particle Swarm Optimization Algorithm with Elitist Breeding for Unconstrained Optimization.Comput Intell Neurosci. 2015;2015:326431. doi: 10.1155/2015/326431. Epub 2015 May 10. Comput Intell Neurosci. 2015. PMID: 26064085 Free PMC article.
-
An Adaptive Cultural Algorithm with Improved Quantum-behaved Particle Swarm Optimization for Sonar Image Detection.Sci Rep. 2017 Dec 18;7(1):17733. doi: 10.1038/s41598-017-17945-3. Sci Rep. 2017. PMID: 29255162 Free PMC article.
-
A Swarm Optimization Genetic Algorithm Based on Quantum-Behaved Particle Swarm Optimization.Comput Intell Neurosci. 2017;2017:2782679. doi: 10.1155/2017/2782679. Epub 2017 May 25. Comput Intell Neurosci. 2017. PMID: 28630619 Free PMC article.
-
Prediction on transmission trajectory of COVID-19 based on particle swarm algorithm.Pattern Recognit Lett. 2021 Dec;152:70-78. doi: 10.1016/j.patrec.2021.09.003. Epub 2021 Sep 15. Pattern Recognit Lett. 2021. PMID: 34538991 Free PMC article.
-
Review of fractional epidemic models.Appl Math Model. 2021 Sep;97:281-307. doi: 10.1016/j.apm.2021.03.044. Epub 2021 Apr 20. Appl Math Model. 2021. PMID: 33897091 Free PMC article. Review.
Cited by
-
Applications of nature-inspired metaheuristic algorithms for tackling optimization problems across disciplines.Sci Rep. 2024 Apr 24;14(1):9403. doi: 10.1038/s41598-024-56670-6. Sci Rep. 2024. PMID: 38658593 Free PMC article.
References
-
- Souza W., Buss L.F., Candido D., et al. Epidemiological and clinical characteristics of the COVID-19 epidemic in Brazil. Nat. Hum. Behav. 2020;4(8):856–895. - PubMed
-
- Hao X., Cheng S., Wu D., et al. Reconstruction of the full transmission dynamics of COVID-19 in Wuhan. Nature. 2020;584(2020):1–7. - PubMed
LinkOut - more resources
Full Text Sources
