Marginal speed confinement resolves the conflict between correlation and control in collective behaviour
- PMID: 35538068
- PMCID: PMC9090766
- DOI: 10.1038/s41467-022-29883-4
Marginal speed confinement resolves the conflict between correlation and control in collective behaviour
Abstract
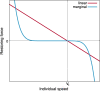
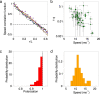
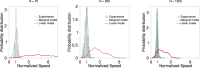
Speed fluctuations of individual birds in natural flocks are moderate, due to the aerodynamic and biomechanical constraints of flight. Yet the spatial correlations of such fluctuations are scale-free, namely they have a range as wide as the entire group, a property linked to the capacity of the system to collectively respond to external perturbations. Scale-free correlations and moderate fluctuations set conflicting constraints on the mechanism controlling the speed of each agent, as the factors boosting correlation amplify fluctuations, and vice versa. Here, using a statistical field theory approach, we suggest that a marginal speed confinement that ignores small deviations from the natural reference value while ferociously suppressing larger speed fluctuations, is able to reconcile scale-free correlations with biologically acceptable group's speed. We validate our theoretical predictions by comparing them with field experimental data on starling flocks with group sizes spanning an unprecedented interval of over two orders of magnitude.
© 2022. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures

Similar articles
-
Statistical mechanics for natural flocks of birds.Proc Natl Acad Sci U S A. 2012 Mar 27;109(13):4786-91. doi: 10.1073/pnas.1118633109. Epub 2012 Mar 16. Proc Natl Acad Sci U S A. 2012. PMID: 22427355 Free PMC article.
-
Scale-free correlations in starling flocks.Proc Natl Acad Sci U S A. 2010 Jun 29;107(26):11865-70. doi: 10.1073/pnas.1005766107. Epub 2010 Jun 14. Proc Natl Acad Sci U S A. 2010. PMID: 20547832 Free PMC article.
-
Social interactions dominate speed control in poising natural flocks near criticality.Proc Natl Acad Sci U S A. 2014 May 20;111(20):7212-7. doi: 10.1073/pnas.1324045111. Epub 2014 May 1. Proc Natl Acad Sci U S A. 2014. PMID: 24785504 Free PMC article.
-
New statistical tools for analyzing the structure of animal groups.Math Biosci. 2008 Jul-Aug;214(1-2):32-7. doi: 10.1016/j.mbs.2008.05.006. Epub 2008 May 27. Math Biosci. 2008. PMID: 18586280
-
Estimating power curves of flying vertebrates.J Exp Biol. 1999 Dec;202(Pt 23):3449-61. doi: 10.1242/jeb.202.23.3449. J Exp Biol. 1999. PMID: 10562528 Review.
Cited by
-
Synchronization in collectively moving inanimate and living active matter.Nat Commun. 2023 Sep 13;14(1):5633. doi: 10.1038/s41467-023-41432-1. Nat Commun. 2023. PMID: 37704595 Free PMC article.
-
Exploring the criticality hypothesis using programmable swarm robots with Vicsek-like interactions.J R Soc Interface. 2023 Jul;20(204):20230176. doi: 10.1098/rsif.2023.0176. Epub 2023 Jul 19. J R Soc Interface. 2023. PMID: 37464802 Free PMC article.
-
Functional duality in group criticality via ambiguous interactions.PLoS Comput Biol. 2023 Feb 15;19(2):e1010869. doi: 10.1371/journal.pcbi.1010869. eCollection 2023 Feb. PLoS Comput Biol. 2023. PMID: 36791061 Free PMC article.
-
Body orientation change of neighbors leads to scale-free correlation in collective motion.Nat Commun. 2024 Oct 17;15(1):8968. doi: 10.1038/s41467-024-53361-8. Nat Commun. 2024. PMID: 39420172 Free PMC article.
-
Perception of motion salience shapes the emergence of collective motions.Nat Commun. 2024 Jun 5;15(1):4779. doi: 10.1038/s41467-024-49151-x. Nat Commun. 2024. PMID: 38839782 Free PMC article.
References
-
- Reynolds, C. W. Flocks, herds and schools: a distributed behavioral model. In Proc. 14th Annual Conference on Computer Graphics and Interactive Techniques (ed. Stone, M. C.) 25–34 (Association for Computing Machinery, 1987).
-
- Heppner F, Grenander U. A stochastic nonlinear model for coordinated bird flocks. Ubiquity Chaos. 1990;233:238.
-
- Huth A, Wissel C. The simulation of the movement of fish schools. J. Theor. Biol. 1992;156:365–385. doi: 10.1016/S0022-5193(05)80681-2. - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

