The Probability of Joint Monophyly of Samples of Gene Lineages for All Species in an Arbitrary Species Tree
- PMID: 35544237
- PMCID: PMC9464369
- DOI: 10.1089/cmb.2021.0647
The Probability of Joint Monophyly of Samples of Gene Lineages for All Species in an Arbitrary Species Tree
Abstract
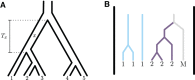
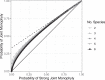
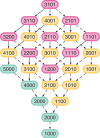
Monophyly is a feature of a set of genetic lineages in which every lineage in the set is more closely related to all other members of the set than it is to any lineage outside the set. Multiple sets of lineages that are separately monophyletic are said to be reciprocally monophyletic, or jointly monophyletic. The prevalence of reciprocal monophyly, or joint monophyly (JM), has been used to evaluate phylogenetic and phylogeographic hypotheses, as well as to delimit species. These applications often make use of a probability of JM under models of gene lineage evolution. Studies in coalescent theory have computed this JM probability for small numbers of separate groups in arbitrary species trees and for arbitrary numbers of separate groups in trivial species trees. In this study, generalizing existing results on monophyly probabilities under the multispecies coalescent, we derive the probability of JM for arbitrary numbers of separate groups in arbitrary species trees. We illustrate how our result collapses to previously examined cases. We also study the effect of tree height, sample size, and number of species on the probability of JM. We obtain relatively simple lower and upper bounds on the JM probability. Our results expand the scope of JM calculations beyond small numbers of species, subsuming past formulas that have been used in simpler cases.
Keywords: coalescent; gene tree; monophyly; probability; species tree.
Conflict of interest statement
The authors declare they have no conflicting financial interests.
Figures





Similar articles
-
The probability of monophyly of a sample of gene lineages on a species tree.Proc Natl Acad Sci U S A. 2016 Jul 19;113(29):8002-9. doi: 10.1073/pnas.1601074113. Epub 2016 Jul 18. Proc Natl Acad Sci U S A. 2016. PMID: 27432988 Free PMC article.
-
The probability of reciprocal monophyly of gene lineages in three and four species.Theor Popul Biol. 2019 Oct;129:133-147. doi: 10.1016/j.tpb.2018.04.004. Epub 2018 May 3. Theor Popul Biol. 2019. PMID: 29729946 Free PMC article.
-
The shapes of neutral gene genealogies in two species: probabilities of monophyly, paraphyly, and polyphyly in a coalescent model.Evolution. 2003 Jul;57(7):1465-77. doi: 10.1111/j.0014-3820.2003.tb00355.x. Evolution. 2003. PMID: 12940352
-
Challenges in Species Tree Estimation Under the Multispecies Coalescent Model.Genetics. 2016 Dec;204(4):1353-1368. doi: 10.1534/genetics.116.190173. Genetics. 2016. PMID: 27927902 Free PMC article. Review.
-
Coalescent methods for estimating phylogenetic trees.Mol Phylogenet Evol. 2009 Oct;53(1):320-8. doi: 10.1016/j.ympev.2009.05.033. Epub 2009 Jun 6. Mol Phylogenet Evol. 2009. PMID: 19501178 Review.
Cited by
-
All galls are divided into three or more parts: recursive enumeration of labeled histories for galled trees.Algorithms Mol Biol. 2023 Feb 13;18(1):1. doi: 10.1186/s13015-023-00224-4. Algorithms Mol Biol. 2023. PMID: 36782318 Free PMC article.
References
-
- Arbogast, B.S., Edwards, S.V., Wakeley, J., et al. . 2002. Estimating divergence times from molecular data on phylogenetic and population genetic timescales. Ann. Rev. Ecol. Syst. 33, 707–740.
-
- Baker, A.J., Tavares, E.S., and Elbourne, R.F.. 2009. Countering criticisms of single mitochondrial DNA gene barcoding in birds. Mol. Ecol. Resour. 9, 257–268. - PubMed
-
- Birky, C.W., Wolf, C., Maughan, H., et al. . 2005. Speciation and selection without sex. Hydrobiologia. 546, 29–45.
-
- Brown, J.K. 1994. Probabilities of evolutionary trees. Syst. Biol. 43, 78–91.
Appendix Reference
-
- Grimmett, G.R., and Stirzaker, D.S.. 2020. Probability and Random Processes, 4th ed. Oxford University Press, Oxford, UK.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

