Numerical simulations of wall contact angle effects on droplet size during step emulsification
- PMID: 35548132
- PMCID: PMC9086337
- DOI: 10.1039/c8ra06837b
Numerical simulations of wall contact angle effects on droplet size during step emulsification
Abstract
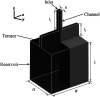
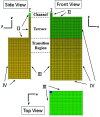
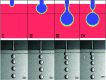
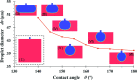
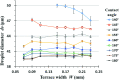
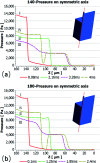
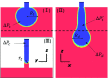
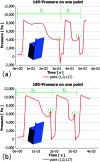
Terrace-based microfluidic devices are currently used to prepare highly monodisperse micro-droplets. Droplets are generated due to the spontaneous pressure drop induced by the Laplace pressure, and so the flow rate of a dispersed phase has little effect on droplet size. As a result, control over the droplet is limited once a step emulsification device has been fabricated. In this work, a terrace model was established to study the effect of the wall contact angle on droplet size based on computational fluid dynamics simulations. The results for contact angles from 140° to 180° show that a lower contact angle induces wall-wetting, increasing the droplet size. The Laplace pressure equations for droplet generation were determined based on combining pressure change curves with theoretical analyses, to provide a theoretical basis for controlling and handling droplets generated through step emulsification.
This journal is © The Royal Society of Chemistry.
Conflict of interest statement
There are no conflicts to declare.
Figures
Similar articles
-
Surfactant solutions and porous substrates: spreading and imbibition.Adv Colloid Interface Sci. 2004 Nov 29;111(1-2):3-27. doi: 10.1016/j.cis.2004.07.007. Adv Colloid Interface Sci. 2004. PMID: 15571660
-
Monodisperse droplet formation by spontaneous and interaction based mechanisms in partitioned EDGE microfluidic device.Sci Rep. 2019 May 24;9(1):7820. doi: 10.1038/s41598-019-44239-7. Sci Rep. 2019. PMID: 31127142 Free PMC article.
-
Effect of Intersection Angle of Input Channels in Droplet Generators.Molecules. 2022 Mar 9;27(6):1791. doi: 10.3390/molecules27061791. Molecules. 2022. PMID: 35335156 Free PMC article.
-
Linking Findings in Microfluidics to Membrane Emulsification Process Design: The Importance of Wettability and Component Interactions with Interfaces.Membranes (Basel). 2016 May 11;6(2):26. doi: 10.3390/membranes6020026. Membranes (Basel). 2016. PMID: 27187484 Free PMC article. Review.
-
Recent advances in droplet wetting and evaporation.Chem Soc Rev. 2018 Jan 22;47(2):558-585. doi: 10.1039/c6cs00902f. Chem Soc Rev. 2018. PMID: 29090296 Review.
Cited by
-
Effects of wall velocity slip on droplet generation in microfluidic T-junctions.RSC Adv. 2019 Jul 26;9(40):23229-23240. doi: 10.1039/c9ra03761f. eCollection 2019 Jul 23. RSC Adv. 2019. PMID: 35514511 Free PMC article.
-
Non-Newtonian Droplet Generation in a Cross-Junction Microfluidic Channel.Polymers (Basel). 2021 Jun 9;13(12):1915. doi: 10.3390/polym13121915. Polymers (Basel). 2021. PMID: 34207574 Free PMC article.
-
Near-Infrared Spectroscopy Coupled with Chemometrics and Artificial Neural Network Modeling for Prediction of Emulsion Droplet Diameters.Micromachines (Basel). 2022 Oct 31;13(11):1876. doi: 10.3390/mi13111876. Micromachines (Basel). 2022. PMID: 36363897 Free PMC article.
References
LinkOut - more resources
Full Text Sources
Research Materials

