Biomarker interaction selection and disease detection based on multivariate gain ratio

Abstract

Background: Disease detection is an important aspect of biotherapy. With the development of biotechnology and computer technology, there are many methods to detect disease based on single biomarker. However, biomarker does not influence disease alone in some cases. It's the interaction between biomarkers that determines disease status. The existing influence measure I-score is used to evaluate the importance of interaction in determining disease status, but there is a deviation about the number of variables in interaction when applying I-score. To solve the problem, we propose a new influence measure Multivariate Gain Ratio (MGR) based on Gain Ratio (GR) of single-variate, which provides us with multivariate combination called interaction.

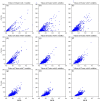
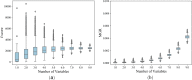
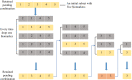
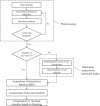
Results: We propose a preprocessing verification algorithm based on partial predictor variables to select an appropriate preprocessing method. In this paper, an algorithm for selecting key interactions of biomarkers and applying key interactions to construct a disease detection model is provided. MGR is more credible than I-score in the case of interaction containing small number of variables. Our method behaves better with average accuracy [Formula: see text] than I-score of [Formula: see text] in Breast Cancer Wisconsin (Diagnostic) Dataset. Compared to the classification results [Formula: see text] based on all predictor variables, MGR identifies the true main biomarkers and realizes the dimension reduction. In Leukemia Dataset, the experiment results show the effectiveness of MGR with the accuracy of [Formula: see text] compared to I-score with accuracy [Formula: see text]. The results can be explained by the nature of MGR and I-score mentioned above because every key interaction contains a small number of variables in Leukemia Dataset.

Conclusions: MGR is effective for selecting important biomarkers and biomarker interactions even in high-dimension feature space in which the interaction could contain more than two biomarkers. The prediction ability of interactions selected by MGR is better than I-score in the case of interaction containing small number of variables. MGR is generally applicable to various types of biomarker datasets including cell nuclei, gene, SNPs and protein datasets.

Keywords: Biomarker interaction; Disease detection; Multivariate gain ratio.

Fig. 1

Scatter plots of correlation between I-score and MGR. For example, when $p=1$, we sample one variable as an interaction from 3571 predictor variables 500 times. We document I-score and MGR of the interaction as a numerical pair. Then we get the scatter plot Values of Cluster with 1 variable in a. I-score and MGR are consistent in the nature of growth

Fig. 2

Variation of I-score and MGR with variable number in range 1 and 9. a I-score varies with the number of variables in logarithmic function form, while MGR is in the form of the exponential function as shown in b

Fig. 3

Illustration of BDA. In this example, we randomly select five biomarkers $\left\{x_{b_1},,,x_{b_2},,,x_{b_3},,,x_{b_4},,,x_{b_5}\right\}$ as the initial subset. For ease of display, the biomarkers $\left\{x_{b_1},,,x_{b_2},,,x_{b_3},,,x_{b_4},,,x_{b_5}\right\}$ is represented by the subscript interaction $\left\{1,,,2,,,3,,,4,,,5\right\}$

Fig. 4

Flowchart of proposed interaction selection and classifier construction. There are five main steps in the algorithm including preprocessing, dimension reduction by interacted triples, generation of interactions based on BDA, construction of the sub-classifier, construction of the final classifier based on Boosting

Fig. 5

Distributions of interactions selected from Breast Cancer Wisconsin (Diagnostic) Dataset with different number of variables. a We get 40 key interactions totally after 5-CV Experiments based on I-score, where there are 8 interactions with one predictor variable and 32 interactions with two predictor variables. b We get 40 key interactions totally after 5-CV Experiments based on MGR, where every one of the 40 interactions contains one predictor variable

Fig. 6

Distributions of interactions selected from Leukemia Dataset with different number of variables. a We get 159 key interactions totally after 5-CV Experiments based on I-score, where there are 4 interactions with two predictor variables and 15 interactions with three predictor variables until 4 interactions with seven predictor variables. b We get 119 key interactions totally after 5-CV Experiments based on MGR and the distribution of the interactions is shown in the plot