High-performance superconducting quantum processors via laser annealing of transmon qubits

Abstract

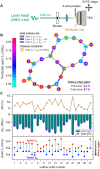
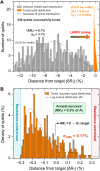
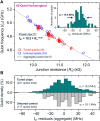
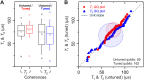
Scaling the number of qubits while maintaining high-fidelity quantum gates remains a key challenge for quantum computing. Presently, superconducting quantum processors with >50 qubits are actively available. For these systems, fixed-frequency transmons are attractive because of their long coherence and noise immunity. However, scaling fixed-frequency architectures proves challenging because of precise relative frequency requirements. Here, we use laser annealing to selectively tune transmon qubits into desired frequency patterns. Statistics over hundreds of annealed qubits demonstrate an empirical tuning precision of 18.5 MHz, with no measurable impact on qubit coherence. We quantify gate error statistics on a tuned 65-qubit processor, with median two-qubit gate fidelity of 98.7%. Baseline tuning statistics yield a frequency-equivalent resistance precision of 4.7 MHz, sufficient for high-yield scaling beyond 10³ qubit levels. Moving forward, we anticipate selective laser annealing to play a central role in scaling fixed-frequency architectures.

Fig. 1.. Example of a LASIQ anneal process.

(A) Outline of the laser trimming setup (23). A 532-nm second-harmonic generation laser is sequentially focused on the junctions of a multiqubit quantum processor, with thermal annealing to selectively decrease qubit frequencies (f₀₁) for collision avoidance. (B) Example of a tuned 27-qubit Falcon lattice. Final predicted f₀₁ are depicted as a heatmap, with initial high-risk NN collision pairs highlighted, and orange outlines indicating initial f₀₁ above the bandwidth of Purcell protection. After LASIQ, collision and frequency constraints are resolved. (C) Detail of qubit anneals. The bottom panel indicates the initial (red) and final (blue) predicted f₀₁ showing the qubits tuned to distinct frequency set points. The middle panel indicates the tuning distance (monotonic negative shifts), along with the desired target shifts (purple diamonds), with an RMS deviation (i.e., frequency-equivalent resistance tuning precision) of 4.8 MHz, as determined from empirical f₀₁(R_n) correlations. The top panel depicts the corresponding junction resistance shifts, achieving tuning ranges up to 14.2%.

Fig. 2.. LASIQ tuning outcome statistics.

(A) Initial distribution (gray) of qubits that were successfully tuned to target (orange). The distance from target δR_T is the tuning differential normalized to the final target resistance R_T. Orange bars indicate the final distribution (20× reduced bin width for clarity) and show the 349 qubits tuned to success. (B) Expanded view of the orange distribution shown in (A). Anneal success is defined as a tuned resistance within 0.3% of R_T, which was reached by all displayed qubits, and 89.5% of the 390 tuned qubits (details in the Supplementary Materials). The blue/red regions indicate undershoot/overshoot, respectively. A log-normal fit is shown by the black curve, which supports the interpretation of LASIQ tuning as an incremental resistance growth process.

Fig. 3.. Frequency assignment precision based on statistical aggregates of tuned 27-qubit Falcon and 65-qubit Hummingbird processors.

(A) Resistance (R_n) to frequency (f₀₁) correlation for a tuned Hummingbird processor. Cryogenic f₀₁ measurements are plotted against measured junction resistances R_n, with a power-law curve superimposed on the measured data. Both tuned (49 qubits) and untuned (16) qubits are depicted. The inset shows a histogram of residuals with an SD of 18.6 MHz, indicating the practical precision to which we may assign qubit frequencies. (B) The top panel shows statistical precision analysis performed for a total of 241 tuned qubits from a combination of Falcon and Hummingbird chips, with aggregate f₀₁ residuals from individual power-law regressions for each chip. The bottom panel shows identical analysis performed for 117 untuned qubits from both processor families. Cryogenic f₀₁ measurements yield 18.5- and 18.1-MHz spread for tuned and untuned qubits, respectively, indicating that the LASIQ process does not significantly affect the overall spread of qubit frequencies before preparatory chip cleaning, bonding, and cooldown processes.

Fig. 4.. Impact of LASIQ tuning on qubit relaxation (T₁, red) and dephasing (T₂, blue), using composite (partially tuned) Hummingbird processors.

Qubit coherences on four Hummingbird chips are analyzed. On each chip, both untuned and tuned qubits were simultaneously measured, for a total statistical sample of 59 untuned and 162 tuned qubits. (A) Box plots of T₁ and T₂ distributions (with interquartile box range, 10 to 90% whiskers, 1 to 99% outliers indicated by crosses and minima/maxima by horizontal markers). Coherence distributions show no statistically significant difference in untuned as compared with LASIQ-tuned qubit populations. (B) Illustrates this comparison as a quantile-quantile (QQ) plot of the T₁ and T₂ distributions. Each point represents a comparison between estimated quantiles from the set of 59 untuned qubits against the interpolated quantiles of the 162 tuned qubits. Good linearity with respect to unit slope indicates a close match of the coherence distributions in tuned and untuned qubit populations. Mean values agree robustly within statistical error bounds. For tuned (untuned) qubits, 〈T₁〉 = 80 ± 16 μs (76 ± 15 μs) and 〈T₂〉 = 68 ± 25 μs (70 ± 26 μs). The shaded ovals are centered on the mean coherence times and have 1-σ extent in relaxation and dephasing times.

Fig. 5.. Gate errors of a 65-qubit Hummingbird processor after LASIQ tuning.

(A) Distribution of tuned two-qubit f₀₁ separation (orange), along with the initial (pre-LASIQ) distribution (blue), indicating high density of collisions and gate errors before LASIQ tuning. (B) Achieved ZZ distribution after LASIQ tuning, indicating well-tailored separation near null-detuning (type 1 NN collision), while maintaining a tight ZZ spread with 69-kHz median. A kernel density estimator (KDE) is used to calculate the ZZ probability density (right). (C) Measured CNOT (Controlled NOT) gate errors as a function of two-qubit detuning (orange points), yielding a median gate fidelity of 98.7% for the LASIQ-tuned Hummingbird (the corresponding KDE distribution of gate errors is shown on the right panel). The shaded (gray) regions indicate approximative error-rate projections based on CR gate error modeling (35), incorporating typical qubit interaction parameters (frequency and anharmonicity, qubit coupling, and gate times), with optional rotary echo pulsing for error minimization.