Actin Stress Fibers Response and Adaptation under Stretch

Abstract

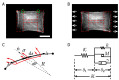
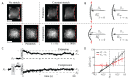
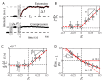
One of the many effects of soft tissues under mechanical solicitation in the cellular damage produced by highly localized strain. Here, we study the response of peripheral stress fibers (SFs) to external stretch in mammalian cells, plated onto deformable micropatterned substrates. A local fluorescence analysis reveals that an adaptation response is observed at the vicinity of the focal adhesion sites (FAs) due to its mechanosensor function. The response depends on the type of mechanical stress, from a Maxwell-type material in compression to a complex scenario in extension, where a mechanotransduction and a self-healing process takes place in order to prevent the induced severing of the SF. A model is proposed to take into account the effect of the applied stretch on the mechanics of the SF, from which relevant parameters of the healing process are obtained. In contrast, the repair of the actin bundle occurs at the weak point of the SF and depends on the amount of applied strain. As a result, the SFs display strain-softening features due to the incorporation of new actin material into the bundle. In contrast, the response under compression shows a reorganization with a constant actin material suggesting a gliding process of the SFs by the myosin II motors.

Keywords: SF response; actin stress fibers; cell mechanics.

Figure 1

F-actin-labeled RPE-1 cells on PLL-g-PEG/fibronectin patterns. (A,B) Cells with main F-actin bundles at the free edge before stretch and the same cell after 15 min at a constant stretch (H-like pattern is displayed on segmented red lines, while the green circles target the FAs location). The experimental apparatus stretches the PDMS substrate, exerting tension on the cell and the stress fibers as well. Scale bar $20\mathsf{\mu }$m. (C) Sketch of an F-actin bundle between two anchored points (FAs), with radius of curvature R, cortical tension $\sigma$ and the line tension $\lambda$ along the bundle. (D) Mechanical representation of the SF.

Figure 2

Radius of curvature of SFs vs. the applied strain. (A) Two examples of RPE-1 cells plated on H-like patterns before and during the applied stretch. Scale bar $20\mathsf{\mu }$m. (B) Sketch of the SF and the definition of the radius of curvature. (C) Response of the radius of curvature as a function of time for extension and compression conditions. Note that the initial radius of curvature for compression experiments corresponds to a prestretched state with initial radius $R_0^p$, whereas $R_0^{+}$ and $R_{\infty }$ correspond to the radii just after stretch and after fifteen minutes of constant stretch, respectively. The gray region represents the delay on the observation due to the stretching process at a velocity of $100\mathsf{\mu }$m/s. (D) Radius of curvature difference at short and long time scale (circles and squares symbols) for extension and compression experiments. N = 12 SF for each data point. Notice that the error bars amplitude, in all plots, correspond to the standard deviation (SD); therefore, the uncertainty of the data correspond to the SD value divided by $\sqrt{N}$.

Figure 3

SF intensity response under stretch. (A) Total fluorescent intensity evolution (integrated along the bundle) at a constant stretch applied to the PDMS. (B) Variation of the F-actin intensity as a function of the applied strain. (C) Initial slope of the intensity evolution as a function of the applied strain. (D) Variation of the linear density, defined as the total intensity over the total SF length, a function of the applied strain. N = 12 SF for each data point.

Figure 4

Local analysis of the F-actin intensity kymograph. (A) RPE-1 cell on H-like pattern at constant stretch ($ϵ\approx 0.2$). Scale bar $20\mathsf{\mu }$m. (B) Normalized relative intensity kymograph of the bottom SF (arc-segment 1–2) displays high activity at both ends of the SF, whereas a moderate intensity evolution at the middle section of the bundle. (C) Intensity profiles along the bottom SF for $t=0$ s (blue solid line), $t=150$ s (red solid line) and $t=600$ s (green solid line), respectively. The red square identifies the SF minimum intensity (mSF), whereas the red circle shows the highest F-actin intensity location (FA). (D) F-Actin intensity profile of 14 SFs, where the thick continuous black line represents a sketch of the F-actin bundle, with two focal adhesion sites (FAs) and a valley at the middle section of the SF (mSF). (E) Normalized intensity evolution of the bottom SF computed from the kymograph at the FA region (red circle), whereas (G) displays the evolution at the mSF region (red square). In both cases, the local curvature is shown (gray solid line). Mechanical parameter values were obtained from best fits (red segmented lines) computed using the intensity data and Equation (10). (F,H) Intensity evolution of 14 FAs and 12 mSFs locations at constant stretch. The thick continuous black line represents a sketch of the intensity evolution at these locations.