Theory of Excitons in Atomically Thin Semiconductors: Tight-Binding Approach
- PMID: 35564291
- PMCID: PMC9104105
- DOI: 10.3390/nano12091582
Theory of Excitons in Atomically Thin Semiconductors: Tight-Binding Approach
Abstract
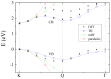
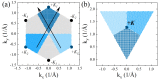
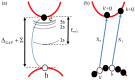
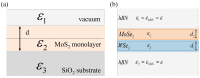
Atomically thin semiconductors from the transition metal dichalcogenide family are materials in which the optical response is dominated by strongly bound excitonic complexes. Here, we present a theory of excitons in two-dimensional semiconductors using a tight-binding model of the electronic structure. In the first part, we review extensive literature on 2D van der Waals materials, with particular focus on their optical response from both experimental and theoretical points of view. In the second part, we discuss our ab initio calculations of the electronic structure of MoS2, representative of a wide class of materials, and review our minimal tight-binding model, which reproduces low-energy physics around the Fermi level and, at the same time, allows for the understanding of their electronic structure. Next, we describe how electron-hole pair excitations from the mean-field-level ground state are constructed. The electron-electron interactions mix the electron-hole pair excitations, resulting in excitonic wave functions and energies obtained by solving the Bethe-Salpeter equation. This is enabled by the efficient computation of the Coulomb matrix elements optimized for two-dimensional crystals. Next, we discuss non-local screening in various geometries usually used in experiments. We conclude with a discussion of the fine structure and excited excitonic spectra. In particular, we discuss the effect of band nesting on the exciton fine structure; Coulomb interactions; and the topology of the wave functions, screening and dielectric environment. Finally, we follow by adding another layer and discuss excitons in heterostructures built from two-dimensional semiconductors.
Keywords: Bethe–Salpeter equation; excitons; tight-binding; transition metal dichalcogenides.
Conflict of interest statement
The authors declare no conflict of interest.
Figures



Similar articles
-
Phonon Screening of Excitons in Atomically Thin Semiconductors.Phys Rev Lett. 2024 Nov 15;133(20):206901. doi: 10.1103/PhysRevLett.133.206901. Phys Rev Lett. 2024. PMID: 39626743
-
Observation of room temperature excitons in an atomically thin topological insulator.Nat Commun. 2022 Oct 23;13(1):6313. doi: 10.1038/s41467-022-33822-8. Nat Commun. 2022. PMID: 36274087 Free PMC article.
-
Interlayer Coupling and Gate-Tunable Excitons in Transition Metal Dichalcogenide Heterostructures.Nano Lett. 2017 Dec 13;17(12):7809-7813. doi: 10.1021/acs.nanolett.7b04021. Epub 2017 Nov 30. Nano Lett. 2017. PMID: 29164895
-
Ultrafast dynamics in van der Waals heterostructures.Nat Nanotechnol. 2018 Nov;13(11):994-1003. doi: 10.1038/s41565-018-0298-5. Epub 2018 Nov 5. Nat Nanotechnol. 2018. PMID: 30397296 Review.
-
Retracted Article: Physics of excitons and their transport in two dimensional transition metal dichalcogenide semiconductors.RSC Adv. 2019 Aug 16;9(44):25439-25461. doi: 10.1039/c9ra03769a. eCollection 2019 Aug 13. RSC Adv. 2019. PMID: 35530097 Free PMC article. Review.
Cited by
-
Topologically Protected Photovoltaics in Bi Nanoribbons.Nano Lett. 2024 Jun 5;24(22):6651-6657. doi: 10.1021/acs.nanolett.4c01277. Epub 2024 May 28. Nano Lett. 2024. PMID: 38804328 Free PMC article.
-
3D hydrogen-like screening effect on excitons in hBN-encapsulated monolayer transition metal dichalcogenides.Sci Rep. 2024 Nov 8;14(1):27286. doi: 10.1038/s41598-024-77625-x. Sci Rep. 2024. PMID: 39516513 Free PMC article.
-
Excitons and Phonons in Two-Dimensional Materials: From Fundamental to Applications.Nanomaterials (Basel). 2023 Nov 29;13(23):3047. doi: 10.3390/nano13233047. Nanomaterials (Basel). 2023. PMID: 38063743 Free PMC article.
-
Valley-spin polarization at zero magnetic field induced by strong hole-hole interactions in monolayer WSe2.Sci Adv. 2025 May 9;11(19):eadu4696. doi: 10.1126/sciadv.adu4696. Epub 2025 May 7. Sci Adv. 2025. PMID: 40333968 Free PMC article.
References
-
- Wallace P.R. The Band Theory of Graphite. Phys. Rev. 1947;71:622–634. doi: 10.1103/PhysRev.71.622. - DOI
-
- Connell G., Wilson J., Yoffe A. Effects of pressure and temperature on exciton absorption and band structure of layer crystals: Molybdenum disulphide. J. Phys. Chem. Solids. 1969;30:287–296. doi: 10.1016/0022-3697(69)90310-2. - DOI
-
- Wilson J., Yoffe A. The transition metal dichalcogenides discussion and interpretation of the observed optical, electrical and structural properties. Adv. Phys. 1969;18:193–335. doi: 10.1080/00018736900101307. - DOI
Publication types
Grants and funding
- PPI/APM/2019/1/00085/U/00001/Polish National Agency for Academic Exchange (NAWA)
- QC2DM Strategic Grant No. STPG-521420/Natural Sciences and Engineering Research Council
- Discovery Grant No. RGPIN- 2019-05714/Natural Sciences and Engineering Research Council
- University of Ottawa Research Chair in Quantum Theory of Quantum Materials, Nanostructures, and Devices
LinkOut - more resources
Full Text Sources

