Spatial-dependent quantum dot-photon entanglement via tunneling effect
- PMID: 35568700
- PMCID: PMC9107499
- DOI: 10.1038/s41598-022-11810-8
Spatial-dependent quantum dot-photon entanglement via tunneling effect
Abstract
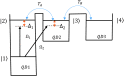
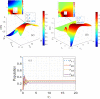
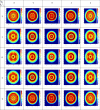
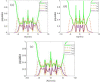
Utilizing the vortex beams, we investigate the entanglement between the triple-quantum dot molecule and its spontaneous emission field. We present the spatially dependent quantum dot-photon entanglement created by Laguerre-Gaussian (LG) fields. The degree of position-dependent entanglement (DEM) is controlled by the angular momentum of the LG light and the quantum tunneling effect created by the gate voltage. Various spatial-dependent entanglement distribution is reached just by the magnitude and the sign of the orbital angular momentum (OAM) of the optical vortex beam.
© 2022. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures


Similar articles
-
Spatially dependent atom-photon entanglement.Sci Rep. 2018 Sep 14;8(1):13840. doi: 10.1038/s41598-018-32051-8. Sci Rep. 2018. PMID: 30218077 Free PMC article.
-
Voltage-controlled two-dimensional Fresnel diffraction pattern in quantum dot molecules.Sci Rep. 2024 Mar 9;14(1):5815. doi: 10.1038/s41598-024-55204-4. Sci Rep. 2024. PMID: 38461176 Free PMC article.
-
Enhancing and flattening multiplexed quantum entanglement by utilizing perfect vortex modes.Opt Lett. 2023 Apr 1;48(7):1782-1785. doi: 10.1364/OL.482249. Opt Lett. 2023. PMID: 37221765
-
Orbital angular momentum of photons and the entanglement of Laguerre-Gaussian modes.Philos Trans A Math Phys Eng Sci. 2017 Feb 28;375(2087):20150442. doi: 10.1098/rsta.2015.0442. Philos Trans A Math Phys Eng Sci. 2017. PMID: 28069773 Free PMC article. Review.
-
Manipulation of continuous variable orbital angular momentum squeezing and entanglement by pump shaping.Opt Express. 2023 Jan 30;31(3):3651-3659. doi: 10.1364/OE.479583. Opt Express. 2023. PMID: 36785352
References
-
- Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935;47:777. doi: 10.1103/PhysRev.47.777. - DOI
-
- Boschi D, Branca S, De Martini F, Hardy L, Popescu S. Experimental realization of teleporting an unknown pure Quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1998;80:1121. doi: 10.1103/PhysRevLett.80.1121. - DOI
LinkOut - more resources
Full Text Sources