Penalized weighted proportional hazards model for robust variable selection and outlier detection

Abstract

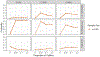
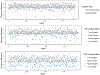
Identifying exceptional responders or nonresponders is an area of increased research interest in precision medicine as these patients may have different biological or molecular features and therefore may respond differently to therapies. Our motivation stems from a real example from a clinical trial where we are interested in characterizing exceptional prostate cancer responders. We investigate the outlier detection and robust regression problem in the sparse proportional hazards model for censored survival outcomes. The main idea is to model the irregularity of each observation by assigning an individual weight to the hazard function. By applying a LASSO-type penalty on both the model parameters and the log transformation of the weight vector, our proposed method is able to perform variable selection and outlier detection simultaneously. The optimization problem can be transformed to a typical penalized maximum partial likelihood problem and thus it is easy to implement. We further extend the proposed method to deal with the potential outlier masking problem caused by censored outcomes. The performance of the proposed estimator is demonstrated with extensive simulation studies and real data analyses in low-dimensional and high-dimensional settings.

Keywords: censoring; high-dimensional data; outlier detection; proportional hazards model; robust estimation; time-to-event outcomes; variable selection.

FIGURE A1

Mean squared errors (MSE) of the standard Cox estimator, the oracle Cox estimator, the robust Cox estimator, the vanilla PAWPH and the PAWPH for β = (1, 2, −1)^T in scenario (a).

FIGURE A2

Outlier detection results from the proposed PAWPH estimator for β = (1, 2, −1)^T in scenario (a). The masking probability for outliers with $0<w<1(\mathcal{M}\text{-})$, the overall masking probability $(\mathcal{M})$, and the swamping probability $(\mathcal{S})$ are plotted in each row, respectively.

FIGURE A3

Mean squared errors (MSE) of the Cox-ALASSO estimator, the oracle Cox-ALASSO estimator, the vanilla PAWPH and the PAWPH for β = (1, 2, −1, 0, 0, 0, 0, 0)^T in scenario (b).

FIGURE A4

Mean squared errors (MSE) of the Cox-ALASSO estimator, the oracle Cox-ALASSO estimator, the vanilla PAWPH and the PAWPH for high-dimensional scenario (c).

FIGURE A5

Mean squared errors (MSE) of the Cox-ALASSO estimator, the oracle Cox-ALASSO estimator, the vanilla PAWPH and the PAWPH for high-dimensional scenario (d).

FIGURE A6

Correctly fitted ratio (CFR) of the Cox-ALASSO estimator, the oracle Cox-ALASSO estimator, the vanilla PAWPH and the PAWPH for β = (1, 2, −1, 0, 0, 0, 0, 0)^T in scenario (b).

FIGURE A7

Correctly fitted ratio (CFR) of the Cox-ALASSO estimator, the oracle Cox-ALASSO estimator, the vanilla PAWPH and the PAWPH for high-dimensional scenario (c).

FIGURE A8

Outlier detection results from the proposed PAWPH estimator for β = (1, 2, −1, 0, 0, 0, 0, 0)^T in scenario (b). The masking probability for outliers with $0<w<1(\mathcal{M}\text{-})$, the overall masking probability $(\mathcal{M})$, and the swamping probability $(\mathcal{S})$ are plotted in each row, respectively.

FIGURE A9

Outlier detection results from the proposed PAWPH estimator for high-dimensional scenario (c). The masking probability for outliers with $0<w<1(\mathcal{M}\text{-})$, the overall masking probability $(\mathcal{M})$, and the swamping probability $(\mathcal{S})$ are plotted in each row, respectively.

FIGURE A10

Outlier detection results from the proposed PAWPH estimator for high-dimensional scenario (d). The masking probability for outliers with $0<w<1(\mathcal{M}\text{-})$, the overall masking probability $(\mathcal{M})$, and the swamping probability $(\mathcal{S})$ are plotted in each row, respectively.

FIGURE 1

Mean squared errors (MSE) of the standard Cox estimator, the oracle Cox estimator, the vanilla PAWPH and the PAWPH for scenarios (b) p = 8 and (c) p = 1000.

FIGURE 2

Correctly fitted ratio (CFR) of the Cox-ALASSO estimator, the oracle Cox-ALASSO estimator, the vanilla PAWPH and the PAWPH for scenarios (b) p = 8 and (c) p = 1000.

FIGURE 3

Outlier detection results from the proposed PAWPH estimator for scenarios (b) p = 8 and (c) p = 1000. The masking probability for outliers with $0<w<1(\mathcal{M}\text{-})$, the overall masking probability $(\mathcal{M})$, and the swamping probability $(\mathcal{S})$ are plotted in each row, respectively.

Figure 4a

Deviance residual plots and outlier detection of the PAWPH with p = 23.

FIGURE 4b

Deviance residual plots and outlier detection of the PAWPH with p = 109.

FIGURE 5

Survival distribution by detected outliers and normal observations for (a) p = 23 and (b) p = 109.

FIGURE 6a

Boxplots of tAUROCs from the testing sets over 100 splits with p = 23. The three panels correspond to 0%, 5% and 10% synthetic contamination on the training sets for each split.

FIGURE 6b

Boxplots of tAUROCs from the testing sets over 100 splits with p = 109. The three panels correspond to 0%, 5% and 10% synthetic contamination on the training sets for each split.