Linear viscoelastic properties of the vertex model for epithelial tissues

Abstract

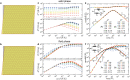
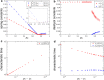
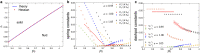
Epithelial tissues act as barriers and, therefore, must repair themselves, respond to environmental changes and grow without compromising their integrity. Consequently, they exhibit complex viscoelastic rheological behavior where constituent cells actively tune their mechanical properties to change the overall response of the tissue, e.g., from solid-like to fluid-like. Mesoscopic mechanical properties of epithelia are commonly modeled with the vertex model. While previous studies have predominantly focused on the rheological properties of the vertex model at long time scales, we systematically studied the full dynamic range by applying small oscillatory shear and bulk deformations in both solid-like and fluid-like phases for regular hexagonal and disordered cell configurations. We found that the shear and bulk responses in the fluid and solid phases can be described by standard spring-dashpot viscoelastic models. Furthermore, the solid-fluid transition can be tuned by applying pre-deformation to the system. Our study provides insights into the mechanisms by which epithelia can regulate their rich rheological behavior.

Fig 1. Epithelial tissue is represented as a polygon tiling of the plane subject to periodic boundary conditions.

We studied the rheology of the vertex model for both (a) regular hexagonal and (b) disordered tilings. Colors represent the number of neighbors of each cell; 4-white, 5-red, 6-gray, 7-blue, 8-yellow.

Fig 2. Storage and loss shear moduli in the solid (top row) and fluid phase (bottom row) for hexagonal tilings.

(a-b) An overlay of the representative reference (grey) and sheared (yellow) configurations in (a) the solid and (b) the fluid phase. The magnitude of the shear is highly exaggerated for demonstration purposes. (c-d) Representative storage (G′) and loss (G″) shear moduli as functions of the shearing frequency, ω₀, for different values of the cell-shape parameter, p₀. Dashed curves are the fits based on (c) the Standard Linear Solid (SLS) model in the solid phase [see Eq (5)] and (d) the Burgers model in the fluid phase [see Eq (8)]. (e-f) The collapse of the moduli curves for different values of p₀ for (e) the solid phase and (f) the fluid phase. The insets show the representation of (e) the SLS model and (f) the Burgers model in terms of the springs and dashpots. The majority of the data corresponds to the system of nearly square shape with N_x = 15 cells in the horizontal direction, and we also show examples of larger systems with N_x = 37 and N_x = 51 cells in the horizontal direction.

Fig 3

(a-b) Fitted values of spring-dashpot models for hexagonal tilings under simple shear. (a) Elastic constants as a function of target cell-shape parameter, p₀. In the solid phase (i.e., for p₀ < p_c ≈ 3.722), fitted values of the spring constants show excellent match with the analytical predictions obtained from Eqs (6) and (7) (dashed lines). Inset shows the spring constants near the critical point. (b) Dashpot viscosity constants as a function of the target cell-shape parameter, p₀. (c-d) Characteristic timescales in (c) the solid and (d) fluid phase for hexagonal tilings obtained from the fitted values of the elastic constant and the dashpot viscosity. The normalization factor t* = γ/(KA₀) sets the unit of time. For the fluid phase (i.e., for p₀ > p_c ≈ 3.722), errorbars correspond to the standard deviation for simulations that were repeated for configurations that correspond to different local energy minima.

Fig 4. Average storage and loss shear moduli in the solid and fluid phase for disordered tilings.

(a,c) Average storage (G′) and loss (G″) shear moduli as functions of the shearing frequency, ω₀, for different values of the cell-shape parameter, p₀, (a) deep in the solid phase and (c) deep in the fluid phase. The error bars represent the standard error of the mean. (b,d) The collapse of the moduli curves for different values of p₀ for (b) the solid phase and (d) the fluid phase. The insets show the representation of (b) the Standard Linear Solid (SLS) model and (d) the Burgers model in terms of the springs and dashpots. (e,f) Average storage (G′) and loss (G″) shear moduli as functions of the shearing frequency, ω₀, for intermediate values of the cell-shape parameter, p₀, in (e) the solid phase and (f) the fluid phase. Dashed curves are the fits based on (a,e) the SLS model in the solid phase [see Eq (5)] and (c,f) the Burgers model in the fluid phase [see Eq (8)]. A representative example of random cell configurations used to produce these plots is shown in Fig 1b.

Fig 5. Fitted values of spring-dashpot models for disordered tilings under simple shear.

(a) Elastic constants as a function of the target cell-shape parameter, p₀. (b) Dashpot viscosity constants as a function of the target cell-shape parameter, p₀. The shaded regions indicate the intermediate regime between the solid and fluid phases.

Fig 6. Loss and storage bulk moduli in the solid (top row) and fluid phase (bottom row) for hexagonal tilings.

(a-b) An overlay of the representative reference (grey) and biaxially deformed (yellow) configurations in (a) the solid and (b) the fluid phase. The magnitude of the bulk deformation is highly exaggerated for demonstration purposes. (c-d) Representative storage (B′) and loss (B″) bulk moduli as functions of the deformation frequency, ω₀, for different values of the cell-shape parameter, p₀. For the solid phase in (c), the loss bulk modulus B″ ≡ 0. For the fluid phase in (d), dashed curves are the fits based on the Standard Linear Solid (SLS) model [see Eq (5)]. (e-f) The collapse of the moduli curves for different values of p₀ for (e) the solid phase and (f) the fluid phase. The insets show the representation of (e) the spring model and (f) the SLS model in terms of the springs and dashpots. In panel (e), B_theory corresponds to the analytical prediction in Eq (9) for the storage bulk modulus in the solid phase.

Fig 7. Fitted values of spring-dashpot models for the system under bulk deformation as a function of the target cell-shape parameter, p₀.

(a) Elastic constants as a function of the target cell-shape parameter, p₀. In the solid phase (p₀ < p_c ≈ 3.722), the bulk storage modulus E_solid agrees with the analytical prediction B_theory in Eq (9) (dashed line). At the solid-fluid transition point (p₀ = p_c ≈ 3.722), it continuously changes to the high frequency limit of the bulk storage modulus, i.e., B′(ω₀ → ∞) = E₁ + E₂, of the fluid phase. The low frequency limit of the bulk storage modulus is B′(ω₀ → 0) = E₂ in the fluid phase. (b) Dashpot viscosity constant as a function of the target cell-shape parameter, p₀. (c) Characteristic timescales in the fluid phase obtained from the fitted values of the elastic constant and the dashpot viscosity. The normalization factor t* = γ/(KA₀) sets the unit of time. For the fluid phase (p₀ > p_c ≈ 3.722), errorbars correspond to the standard deviation for simulations that were repeated for configurations that correspond to different local energy minima.

Fig 8. Average storage and loss bulk moduli in the solid and fluid phase for disordered tilings.

(a,c) Average storage (B′) and loss (B″) bulk moduli as functions of the deformation frequency, ω₀, for different values of the cell-shape parameter, p₀, (a) deep in the solid phase and (c) deep in the fluid phase. The error bars represent the standard error of the mean. (b,d) The collapse of the moduli curves for different values of p₀ for (b) the solid phase and (d) the fluid phase. The insets show the representation of the Standard Linear Solid (SLS) model in terms of the springs and dashpots. (e) Average storage (B′) and loss (B″) bulk moduli as functions of the deformation frequency, ω₀, for intermediate values of the cell-shape parameter, p₀. (f) The collapse of the moduli curves for for intermediate values of the cell-shape parameter, p₀. Dashed curves in (a,c,e) are the fits based on the SLS model [see Eq (5)].

Fig 9. Fitted values of spring-dashpot models for disordered tilings under bulk deformation.

(a) Elastic constants as a function of the target cell-shape parameter, p₀. (b) Dashpot viscosity constant as a function of the target cell-shape parameter, p₀. The shaded regions indicate the intermediate regime between the solid and fluid phases.

Fig 10. Tuning the solid to fluid transition by applying uniaxial pre-deformation.

(a) The solid-fluid transition boundary in the a − p₀ plane, where a measures the amount of uniaxial pre-deformation described by the deformation gradient $\widehat{\mathit{F}}=\left(\begin{array}{cc}a& 0\\ 0& 1\end{array}\right)$. Blue line shows the analytical prediction from Eq (11), which matches the stability analysis with the Hessian matrix (red dots). (b,c) The fitted values of the (b) spring and (c) dashpot constants for the SLS model in the solid phase [see Eq (5)] and the Burgers model in the fluid phase [see Eq (8)] when the system is under uniaxial compression (a = 0.95), no pre-deformation (a = 1.00), and under uniaxial tension (a = 1.05).