A computational model of stereoscopic prey capture in praying mantises
- PMID: 35587948
- PMCID: PMC9159633
- DOI: 10.1371/journal.pcbi.1009666
A computational model of stereoscopic prey capture in praying mantises
Abstract
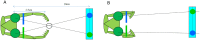
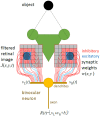
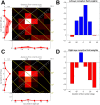
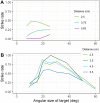
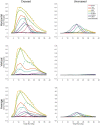
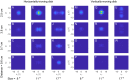
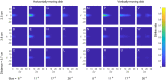
We present a simple model which can account for the stereoscopic sensitivity of praying mantis predatory strikes. The model consists of a single "disparity sensor": a binocular neuron sensitive to stereoscopic disparity and thus to distance from the animal. The model is based closely on the known behavioural and neurophysiological properties of mantis stereopsis. The monocular inputs to the neuron reflect temporal change and are insensitive to contrast sign, making the sensor insensitive to interocular correlation. The monocular receptive fields have a excitatory centre and inhibitory surround, making them tuned to size. The disparity sensor combines inputs from the two eyes linearly, applies a threshold and then an exponent output nonlinearity. The activity of the sensor represents the model mantis's instantaneous probability of striking. We integrate this over the stimulus duration to obtain the expected number of strikes in response to moving targets with different stereoscopic disparity, size and vertical disparity. We optimised the parameters of the model so as to bring its predictions into agreement with our empirical data on mean strike rate as a function of stimulus size and disparity. The model proves capable of reproducing the relatively broad tuning to size and narrow tuning to stereoscopic disparity seen in mantis striking behaviour. Although the model has only a single centre-surround receptive field in each eye, it displays qualitatively the same interaction between size and disparity as we observed in real mantids: the preferred size increases as simulated prey distance increases beyond the preferred distance. We show that this occurs because of a stereoscopic "false match" between the leading edge of the stimulus in one eye and its trailing edge in the other; further work will be required to find whether such false matches occur in real mantises. Importantly, the model also displays realistic responses to stimuli with vertical disparity and to pairs of identical stimuli offering a "ghost match", despite not being fitted to these data. This is the first image-computable model of insect stereopsis, and reproduces key features of both neurophysiology and striking behaviour.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
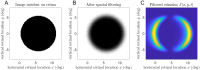
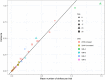

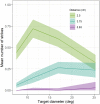




References
-
- Ambrosch K, Kubinger W. Accurate hardware-based stereo vision. Computer Vision and Image Understanding. 2010;114(11):1303–1316. doi: 10.1016/j.cviu.2010.07.008 - DOI
-
- Humenberger M, Zinner C, Weber M, Kubinger W, Vincze M. A fast stereo matching algorithm suitable for embedded real-time systems. Computer Vision and Image Understanding. 2010;114(11):1180–1202. doi: 10.1016/j.cviu.2010.03.012 - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

