Emergent reliability in sensory cortical coding and inter-area communication
- PMID: 35589841
- PMCID: PMC10985415
- DOI: 10.1038/s41586-022-04724-y
Emergent reliability in sensory cortical coding and inter-area communication
Abstract
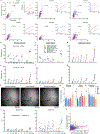
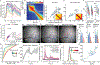
Reliable sensory discrimination must arise from high-fidelity neural representations and communication between brain areas. However, how neocortical sensory processing overcomes the substantial variability of neuronal sensory responses remains undetermined1-6. Here we imaged neuronal activity in eight neocortical areas concurrently and over five days in mice performing a visual discrimination task, yielding longitudinal recordings of more than 21,000 neurons. Analyses revealed a sequence of events across the neocortex starting from a resting state, to early stages of perception, and through the formation of a task response. At rest, the neocortex had one pattern of functional connections, identified through sets of areas that shared activity cofluctuations7,8. Within about 200 ms after the onset of the sensory stimulus, such connections rearranged, with different areas sharing cofluctuations and task-related information. During this short-lived state (approximately 300 ms duration), both inter-area sensory data transmission and the redundancy of sensory encoding peaked, reflecting a transient increase in correlated fluctuations among task-related neurons. By around 0.5 s after stimulus onset, the visual representation reached a more stable form, the structure of which was robust to the prominent, day-to-day variations in the responses of individual cells. About 1 s into stimulus presentation, a global fluctuation mode conveyed the upcoming response of the mouse to every area examined and was orthogonal to modes carrying sensory data. Overall, the neocortex supports sensory performance through brief elevations in sensory coding redundancy near the start of perception, neural population codes that are robust to cellular variability, and widespread inter-area fluctuation modes that transmit sensory data and task responses in non-interfering channels.
© 2022. The Author(s), under exclusive licence to Springer Nature Limited.
Conflict of interest statement
Figures








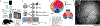



Comment in
-
Volatile neurons unite to stabilize visual experience.Nature. 2022 May;605(7911):625-626. doi: 10.1038/d41586-022-01212-1. Nature. 2022. PMID: 35590062 No abstract available.
References
Additional References for Methods and Extended Data Figures.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

