Emergence of protective behaviour under different risk perceptions to disease spreading

Abstract

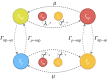
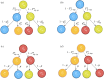
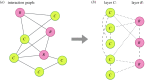
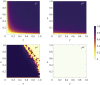
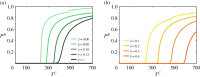
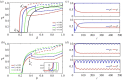
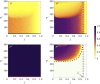
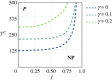
The behaviour of individuals is a main actor in the control of the spread of a communicable disease and, in turn, the spread of an infectious disease can trigger behavioural changes in a population. Here, we study the emergence of individuals' protective behaviours in response to the spread of a disease by considering two different social attitudes within the same population: concerned and risky. Generally speaking, concerned individuals have a larger risk aversion than risky individuals. To study the emergence of protective behaviours, we couple, to the epidemic evolution of a susceptible-infected-susceptible model, a decision game based on the perceived risk of infection. Using this framework, we find the effect of the protection strategy on the epidemic threshold for each of the two subpopulations (concerned and risky), and study under which conditions risky individuals are persuaded to protect themselves or, on the contrary, can take advantage of a herd immunity by remaining healthy without protecting themselves, thanks to the shield provided by concerned individuals. This article is part of the theme issue 'Emergent phenomena in complex physical and socio-technical systems: from cells to societies'.

Keywords: COVID-19; disease spreading; emergence; human behaviour.

Figure 1.

Schematic of model dynamics with given transition probabilities. Dashed lines are related to recovery and infection processes while decision-making processes ($\text{NP}\to P$ and $P\to \text{NP}$ transitions) are represented by dotted lines. (Online version in colour.)

Figure 2.

Transition probability trees for the states $X_y^{i,\alpha }(t)$ at each time step. The root shows initial state at $t$ and the leaves represent the states at the next time $t+1$. The first-row arrows show the $P\to \text{NP}$ and $\text{NP}\to \text{P}$ processes with probabilities ${\Gamma }_{p\to \text{np}}^{i,\alpha }$ and ${\Gamma }_{\text{np}\to p}^{i,\alpha }$. The second-row arrows denote probabilities $\mu$, $q_{\text{np}}^{i,\alpha }$ or $q_p^{i,\alpha }$ governing the changes in the epidemiological states of each node. (Online version in colour.)

Figure 3.

(a) The network consists of eight nodes. Green nodes indicate the concerned $(C)$ agents and red ones are risky $(R)$. (b) A two-layer representation of the model. Concerned (Risky) nodes belong to layer $C$ (layer $R$), connected through intra-layer links, while the risky and concerned nodes are connected through inter-layer links. Intra-layer and inter-layer links are represented by dashed and dotted lines, respectively. (Online version in colour.)

Figure 4.

Panels in the top show, respectively, the phase diagrams for the fraction of concerned and risky agents that are infected ($I^C$ and $I^R$) as a function of $\gamma$ and $\lambda$. From these diagrams it is clear that the healthy phase (according to the colour bar, white=0 corresponding 0% infected) is much larger for the concerned group, especially for small values of $\gamma$. In both populations, the transition from the disease-free regime and the epidemic state is smooth. Panels in the bottom show, respectively, the fraction (according to the colour bar, dark blue=1 corresponding 100% protected) of concerned and risky agents that are protected ($P^C$ and $P^R$) as a function of $\gamma$ and $\lambda$. The diagrams correspond to an ER network with $N=2000$ nodes and mean degree of $⟨k⟩=10$, where $f=0.5$, $T^C=10,\delta =0.01,\mu =0.1$ and $c^R=1$. (Online version in colour.)

Figure 5.

Stationary values for $P^R$ as a function of $T^C$. These diagrams correspond to an ER network with $N=2000$ and $⟨k⟩=10$, where $f=0.5,\delta =0.01,\mu =0.1$ and $c^R=1$. In (a) $\lambda =0.2$ and in (b) $\gamma =0.1$. (Online version in colour.)

Figure 6.

(a,b) Bifurcation diagrams for fraction of $P^R$ as a function of $\delta$. The numerical results are obtained for the ER network with $N=2000$ and $⟨k⟩=10$. Parameters are $T^C=10,\mu =0.1$, $c^R=1$, $f=0.5$, while $\lambda =0.2$ in (a) and $\gamma =0.1$ in (b). Bifurcation points ${\delta }_c$ and ${\delta }_c^{\ast }$ are shown in the figure. Solid lines denote stable fixed-points while dashed-dotted and dashed lines show the lower and upper turning points of stable limit cycles, respectively. (c,d) Numerical results for fraction of protected and infected compartments of both risky and concerned individuals in time $t$ on the ER network with $N=2000$ and $⟨k⟩=10$. Parameters are $T^C=10,\mu =0.1$, $c^R=1,\lambda =0.2,\gamma =0.06$, $f=0.5$ and in (c) $\delta =0.3$ and in (d) $\delta =0.8$. (Online version in colour.)

Figure 7.

Phase diagrams for the infected and protected fraction of the concerned ($I^C$ and $P^C$) and risky ($I^R$ and $P^R$) agents in the space $T^C-f$. Numerical results are obtained on the ER network with $N=2000$ and $⟨k⟩=10$. Other parameters are $\lambda =0.1,\delta =0.01,\mu =0.1$, $c^R=1$ and $\gamma =0.1$. The dashed lines in diagrams for $I^R$ and $P^R$ highlight the estimated value of $f_c$ while the dotted curve is an estimation of the protection threshold. (Online version in colour.)

Figure 8.

Protection threshold curves of the risky agents in $(T^C,f)$ space, for three different values $\gamma =0,0.1$ and 0.2. The region wherein risky agents (do not) protect themselves is labelled as (NP) P which is (bottom) above each curve. (Online version in colour.)

Figure 9.

Phase diagrams for the fraction of infected risky agents, $I_{\text{np}}^R$. The solid line indicates the analytical curve for the epidemic threshold, equation (3.10), while the dashed line indicates the critical value $f_c$, equation (3.11). Parameters are set to $\delta =0$, $\gamma =0$, $\mu =0.1$, $c^R=1$ and $T^C=500$ on the ER network with $N=2000$ and $⟨k⟩=10$. (Online version in colour.)