Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2022 May 6;8(5):e09370.
doi: 10.1016/j.heliyon.2022.e09370. eCollection 2022 May.

Ultra-fine transformation of data for normality

Mohammad M Hamasha  1 , Haneen Ali  2 , Sa'd Hamasha  3 , Abdulaziz Ahmed  4
Affiliations

Ultra-fine transformation of data for normality

Mohammad M Hamasha et al. Heliyon. .

Abstract

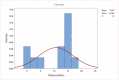
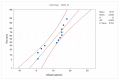
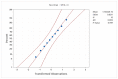
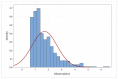
Normally distributed data is crucial for the application of large-scale statistical analysis. To statisticians, the most important assumptions of statistical users are the adequacy of the data and the normal distribution of the data. However, users are constantly forced to deal with unusual data. This includes changing the method used to be less sensitive to non-normal data or transforming that data to normal data. In addition, common mathematical transformation methods (for example, Box-Cox) do not work on complex distributions, and each method works on limited data shapes. In this paper, a novel approach is presented to transform any data into normally distributed data. We refer to our approach as the Ultra-fine transformation method. The article's novelty is that the proposed approach is powerful enough to accurately transform any data with any distribution to the standard normal distribution. Besides this approach's usefulness, it is simple in both theory and in application, and users can easily retrieve the original data from its transformed state. Therefore, we recommend using this method for the data used in the statistical method, even if the data are normal.

Keywords: Data normalization; Normal distribution; Transform for normality; Ultra-fine transformation.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Forward and backward transformation of data.
Figure 2
Figure 2
Histogram of observations for the numerical case 1.
Figure 3
Figure 3
P–P plot of observations for the numerical case 1.
Figure 4
Figure 4
P–P plot of transformed data for the numerical case 1.
Figure 5
Figure 5
Histogram of observations for the numerical case 2.
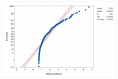
Figure 6
Figure 6
Probability plot of observations for the numerical case 2.
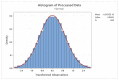
Figure 7
Figure 7
Histogram of transformed observations in numerical case 2.
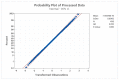
Figure 8
Figure 8
Probability plot of transformed observations in numerical case 2.
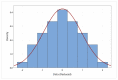
Figure 9
Figure 9
Probability plot of transformed observations in numerical case 2 after reduction.
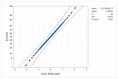
Figure 10
Figure 10
Histogram of transformed observations in question 2 after reduction.
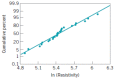
Figure 11
Figure 11
P–P Plot (Figure 6.23, page 265, Montgomery [50].
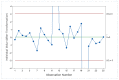
Figure 12
Figure 12
Individual control chart of the transformed data.
See this image and copyright information in PMC

References

    1. Maghami M.M., Bahrami M., Sajadi F.A. On bias reduction estimators of skew-normal and skew-t distributions. J. Appl. Stat. 2020;47(16):3030–3052. - PMC - PubMed
    1. Yalçınkaya A., Şenoğlu B., Yolcu U. Maximum likelihood estimation for the parameters of skew normal distribution using genetic algorithm. Swarm Evol. Comput. 2020;38:127–138.
    1. Nadarajah S. A generalized normal distribution. J. Appl. Stat. 2005;23(7):685–694.
    1. Nadarajah S., Kotzb S. A product Pearson-type VII density distribution. J. Comput. Appl. Math. 2008;211(1):103–113.
    1. Nadarajah S. The product t density distribution arising from the product of two Student’s t PDFs. Stat. Pap. 2009;50:605–615.

LinkOut - more resources