Local topological features of robust supply networks
- PMID: 35615080
- PMCID: PMC9122087
- DOI: 10.1007/s41109-022-00470-2
Local topological features of robust supply networks
Abstract
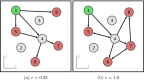
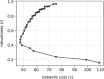
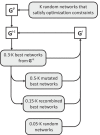
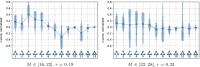
The design of robust supply and distribution systems is one of the fundamental challenges at the interface of network science and logistics. Given the multitude of performance criteria, real-world constraints, and external influences acting upon such a system, even formulating an appropriate research question to address this topic is non-trivial. Here we present an abstraction of a supply and distribution system leading to a minimal model, which only retains stylized facts of the systemic function and, in this way, allows us to investigate the generic properties of robust supply networks. On this level of abstraction, a supply and distribution system is the strategic use of transportation to eliminate mismatches between production patterns (i.e., the amounts of goods produced at each production site of a company) and demand patterns (i.e., the amount of goods consumed at each location). When creating networks based on this paradigm and furthermore requiring the robustness of the system with respect to the loss of transportation routes (edge of the network) we see that robust networks are built from specific sets of subgraphs, while vulnerable networks display a markedly different subgraph composition. Our findings confirm a long-standing hypothesis in the field of network science, namely, that network motifs-statistically over-represented small subgraphs-are informative about the robust functioning of a network. Also, our findings offer a blueprint for enhancing the robustness of real-world supply and distribution systems.
Supplementary information: The online version contains supplementary material available at 10.1007/s41109-022-00470-2.
Keywords: Minimal model; Network motifs; Spatial networks; Supply chain management.
© The Author(s) 2022.
Conflict of interest statement
Competing interestsThe authors declare that they have no competing interests.
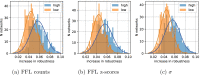
Figures





Similar articles
-
Subgraphs and network motifs in geometric networks.Phys Rev E Stat Nonlin Soft Matter Phys. 2005 Feb;71(2 Pt 2):026117. doi: 10.1103/PhysRevE.71.026117. Epub 2005 Feb 22. Phys Rev E Stat Nonlin Soft Matter Phys. 2005. PMID: 15783388
-
Robust subgraph counting with distribution-free random graph analysis.Phys Rev E. 2021 Oct;104(4-1):044313. doi: 10.1103/PhysRevE.104.044313. Phys Rev E. 2021. PMID: 34781540
-
A flexible robust model for blood supply chain network design problem.Ann Oper Res. 2022 Apr 21:1-26. doi: 10.1007/s10479-022-04673-9. Online ahead of print. Ann Oper Res. 2022. PMID: 35474752 Free PMC article.
-
Network science approach to modelling the topology and robustness of supply chain networks: a review and perspective.Appl Netw Sci. 2017;2(1):33. doi: 10.1007/s41109-017-0053-0. Epub 2017 Oct 10. Appl Netw Sci. 2017. PMID: 30443587 Free PMC article. Review.
-
The architecture of complex weighted networks.Proc Natl Acad Sci U S A. 2004 Mar 16;101(11):3747-52. doi: 10.1073/pnas.0400087101. Epub 2004 Mar 8. Proc Natl Acad Sci U S A. 2004. PMID: 15007165 Free PMC article. Review.
References
-
- Adenso-Díaz B, Mar-Ortiz J, Lozano S. Assessing supply chain robustness to links failure. Int J Prod Res. 2018;56(15):5104–5117. doi: 10.1080/00207543.2017.1419582. - DOI
-
- Albert R, Barabási A-L. Statistical mechanics of complex networks. Rev Mod Phys. 2002;74(1):47. doi: 10.1103/RevModPhys.74.47. - DOI
-
- Aldrighetti R, Battini D, Ivanov D, Zennaro I. Costs of resilience and disruptions in supply chain network design models: a review and future research directions. Int J Prod Econ. 2021;235:108103. doi: 10.1016/j.ijpe.2021.108103. - DOI
-
- Anshelevich E, Dasgupta A, Kleinberg J, Tardos É, Wexler T, Roughgarden T. The price of stability for network design with fair cost allocation. SIAM J Comput. 2008;38(4):1602–1623. doi: 10.1137/070680096. - DOI
LinkOut - more resources
Full Text Sources
