Omnidirectional Manipulation of Microparticles on a Platform Subjected to Circular Motion Applying Dynamic Dry Friction Control

Abstract

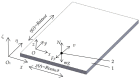
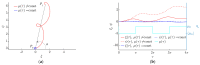
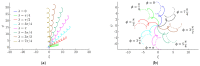
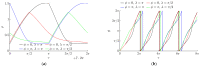
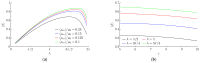
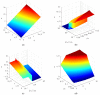
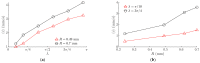
Currently used planar manipulation methods that utilize oscillating surfaces are usually based on asymmetries of time, kinematic, wave, or power types. This paper proposes a method for omnidirectional manipulation of microparticles on a platform subjected to circular motion, where the motion of the particle is achieved and controlled through the asymmetry created by dynamic friction control. The range of angles at which microparticles can be directed, and the average velocity were considered figures of merit. To determine the intrinsic parameters of the system that define the direction and velocity of the particles, a nondimensional mathematical model of the proposed method was developed, and modeling of the manipulation process was carried out. The modeling has shown that it is possible to direct the particle omnidirectionally at any angle over the full 2π range by changing the phase shift between the function governing the circular motion and the dry friction control function. The shape of the trajectory and the average velocity of the particle depend mainly on the width of the dry friction control function. An experimental investigation of omnidirectional manipulation was carried out by implementing the method of dynamic dry friction control. The experiments verified that the asymmetry created by dynamic dry friction control is technically feasible and can be applied for the omnidirectional manipulation of microparticles. The experimental results were consistent with the modeling results and qualitatively confirmed the influence of the control parameters on the motion characteristics predicted by the modeling. The study enriches the classical theories of particle motion on oscillating rigid plates, and it is relevant for the industries that implement various tasks related to assembling, handling, feeding, transporting, or manipulating microparticles.

Keywords: control; dry friction; micromanipulation; microparticles; motion control; oscillating platform; vibrations.

Figure 1

Scheme of the dynamic model of omnidirectional manipulation of particles on a platform subjected to circular motion: (1) platform; (2) particle.

Figure 2

Principle of dynamic dry friction control.

Figure 3

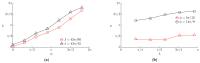
Experimental setup for omnidirectional manipulation applying dynamic dry friction control: (a) General view; (b) Scheme where the following components are shown: (1) platform; (2) elastic rods; (3) piezoelectric actuator; (4) eccentric mechanism; (5) direct current power supply; (6) piezoelectric actuators; (7) manipulation plate; (8) microparticles; (9) optical reference sensor; (10) vibration analyzer; (11) arbitrary waveform generator; (12) piezo linear amplifier; (13) digital oscilloscope; (14) high-speed camera.

Figure 4

Nondimensional displacement of the particle when γ = 4.9, µ₀ = 0.2, ⟨µ_m⟩/µ₀ = 0.25, λ = π, ϕ = 0: (a) motion trajectories of the particle and the angle of displacement α. (b) horizontal ξ and vertical ψ components of the nondimensional displacement vs. the nondimensional time and the variation of the effective dry friction coefficient.

Figure 5

Trajectories of the particle: (a) under different values of λ after 8 cycles of the circular motion of the platform when ϕ = 0, µ₀ = 0.2, ⟨µ_m⟩/µ₀ = 0.25, γ = 4; (b) under different values of the phase shift ϕ after two cycles when µ₀ = 0.2, ⟨µ_m⟩/µ₀ = 0.25, γ = 4.9, λ = π (solid line), λ = 13π/9 (dashed line).

Figure 6

Variation of the angular velocity vector during the period of the eighth cycle of circular motion in polar coordinates when ⟨µ_m⟩/µ₀ = 0.25, γ = 4.9: (a) µ₀ = 0.1; (b) µ₀ = 0.2.

Figure 7

Angular velocity vector vs. the nondimensional time when µ₀ = 0.2, ⟨µ_m⟩/µ₀ = 0.25, γ = 4.9: (a) magnitude ρ during the period of the 8th cycle; (b) phase θ during the first four cycles.

Figure 8

Average nondimensional velocity depending on the following: (a) λ when µ₀ = 0.1, γ = 5, ϕ = 0; (b) γ when µ₀ = 0.1, ϕ = 0, ⟨µ_m⟩/µ₀ = 0.25; (c) ⟨µ_m⟩/µ₀ when γ = 9, ϕ = π/2; (d) µ₀ when ⟨µ_m⟩/µ₀ = 0.25, ϕ = 0, λ = π/2.

Figure 8

Average nondimensional velocity depending on the following: (a) λ when µ₀ = 0.1, γ = 5, ϕ = 0; (b) γ when µ₀ = 0.1, ϕ = 0, ⟨µ_m⟩/µ₀ = 0.25; (c) ⟨µ_m⟩/µ₀ when γ = 9, ϕ = π/2; (d) µ₀ when ⟨µ_m⟩/µ₀ = 0.25, ϕ = 0, λ = π/2.

Figure 9

Average nondimensional velocity depending on the following: (a) λ and γ when µ₀ = 0.1, ⟨µ_m⟩/µ₀ = 0.25, ϕ = 0; (b) ⟨µ_m⟩/µ₀ and µ₀ when γ = 5, ϕ = 0, λ = π; (c) ⟨µ_m⟩/µ₀ and λ when µ₀ = 0.1, γ = 5, ϕ = 0; (d) γ and µ₀ when ⟨µ_m⟩/µ₀ = 4, ϕ = 0, λ = π.

Figure 10

Displacement angle α depending on: (a) ϕ when µ₀ = 0.1, γ = 8.8, ⟨µ_m⟩/µ₀ = 0.25; (b) λ when µ₀ = 0.1, ϕ = 0, ⟨µ_m⟩/µ₀ = 0.25; (c) µ₀ when ⟨µ_m⟩/µ₀ = 0.25, ϕ = 0, λ = π/2; (d) γ when µ₀ = 0.1, ϕ = 0, ⟨µ_m⟩/µ₀ = 0.25.

Figure 11

Displacement angle α depending on: (a) λ and ϕ when µ₀ = 0.1, γ = 8, ⟨µ_m⟩/µ₀ = 0.25; (b) ⟨µ_m⟩/µ₀ and µ₀ when γ = 5, λ = π, ϕ = 0; (c) λ and ⟨µ_m⟩/µ₀ when µ₀ = 0.1, γ = 5, ϕ = 0; (d) µ₀ and γ when ⟨µ_m⟩/µ₀ = 0.25, ϕ = 0, λ = π.

Figure 12

Experimental results of the average velocity depending on the following: (a) λ when ω = 62.83 rad/s, ϕ = 0; (b) the radius of the circular motion of the platform R when ω = 62.83 rad/s, ϕ = 0.

Figure 13

Experimental results of α depending on the following: (a) ϕ when R = 0.49 mm, ω = 62.83 rad/s; (b) λ when R = 0.49 mm, ω = 62.83 rad/s.

Figure 14

Images captured during the experiments: (a) captured trajectory of a single 0603-type MLCC when R = 0.49 mm, ω = 62.83 rad/s, ϕ = 9π/5, λ = 43π/90; (b) two frames separated by a time interval of 0.792 s that were captured during the manipulation of multiple 0603-type MLCC when R = 0.49 mm, ω = 62.83 rad/s, ϕ = 9π/10, λ = 43π/45.