A New Wavelet-Based Privatization Mechanism for Probability Distributions
- PMID: 35632152
- PMCID: PMC9143979
- DOI: 10.3390/s22103743
A New Wavelet-Based Privatization Mechanism for Probability Distributions
Abstract
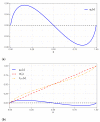
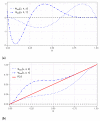
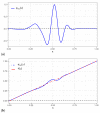
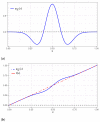
In this paper, we propose a new privatization mechanism based on a naive theory of a perturbation on a probability using wavelets, such as a noise perturbs the signal of a digital image sensor. Wavelets are employed to extract information from a wide range of types of data, including audio signals and images often related to sensors, as unstructured data. Specifically, the cumulative wavelet integral function is defined to build the perturbation on a probability with the help of this function. We show that an arbitrary distribution function additively perturbed is still a distribution function, which can be seen as a privatized distribution, with the privatization mechanism being a wavelet function. Thus, we offer a mathematical method for choosing a suitable probability distribution for data by starting from some guessed initial distribution. Examples of the proposed method are discussed. Computational experiments were carried out using a database-sensor and two related algorithms. Several knowledge areas can benefit from the new approach proposed in this investigation. The areas of artificial intelligence, machine learning, and deep learning constantly need techniques for data fitting, whose areas are closely related to sensors. Therefore, we believe that the proposed privatization mechanism is an important contribution to increasing the spectrum of existing techniques.
Keywords: artificial intelligence; data fitting; database-sensor; digital image sensor; machine learning; perturbation theory; signal-to-noise ratio; statistical modeling; wavelets.
Conflict of interest statement
There are no conflict of interest declared by the authors.
Figures

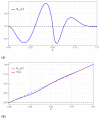
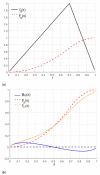
References
-
- Aykroyd R.G., Leiva V., Ruggeri F. Recent developments of control charts, identification of big data sources and future trends of current research. Technol. Forecast. Soc. Change. 2019;144:221–232. doi: 10.1016/j.techfore.2019.01.005. - DOI
-
- Gomez-Deniz E., Leiva V., Calderin-Ojeda E., Chesneau C. A novel claim size distribution based on a Birnbaum-Saunders and gamma mixture capturing extreme values in insurance: Estimation, regression, and applications. Comput. Appl. Math. 2022;41:171. doi: 10.1007/s40314-022-01875-6. - DOI
-
- Bantan R.A.R., Jamal F., Chesneau C., Elgarhy M. Truncated inverted Kumaraswamy generated family of distributions with applications. Entropy. 2019;21:1089. doi: 10.3390/e21111089. - DOI
-
- Johnson N.L., Kotz S., Balakrishnan N. Continuous Univariate Distributions. Volume 1 Wiley; New York, NY, USA: 1994.
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

