Numerical simulation of wave propagation through interfaces using the extended finite element method for magnetic resonance elastography

Abstract

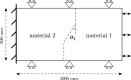
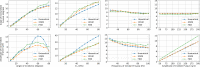
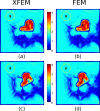
Magnetic resonance elastography (MRE) is an elasticity imaging technique for quantitatively assessing the stiffness of human tissues. In MRE, finite element method (FEM) is widely used for modeling wave propagation and stiffness reconstruction. However, in front of inclusions with complex interfaces, FEM can become burdensome in terms of the model partition and computationally expensive. In this work, we implement a formulation of FEM, known as the eXtended finite element method (XFEM), which is a method used for modeling discontinuity like crack and heterogeneity. Using a level-set method, it makes the interface independent of the mesh, thus relieving the meshing efforts. We investigate this method in two studies: wave propagation across an oblique linear interface and stiffness reconstruction of a random-shape inclusion. In the first study, numerical results by XFEM and FEM models revealing the wave conversion rules at linear interface are presented and successfully compared to the theoretical predictions. The second study, investigated in a pseudo-practical application, demonstrates further the applicability of XFEM in MRE and the convenience, accuracy, and speed of XFEM with respect to FEM. XFEM can be regarded as a promising alternative to FEM for inclusion modeling in MRE.

FIG. 1.

Maxwell form of SLS model.

FIG. 2.

P-S conversion model. It contains a piecewise linear interface represented by the dashed lines separating material 1 on the right side from material 2 on the left side.

FIG. 3.

(Color online) Illustration of mesh of the P-S conversion model by XFEM (a) and FEM (b).

FIG. 4.

Random-shape inclusion model. The random-shape inclusion is represented by dashed lines. (a) aligned inclusion and (b) tilted inclusion.

FIG. 5.

(Color online) Illustration of mesh of the random-shape inclusion model by XFEM and FEM. (a) and (c) present the regular mesh by XFEM for the aligned and tilted inclusion, respectively. (b) and (d) present the mesh by FEM for the aligned and tilted inclusion, respectively, where triangular elements are used to match the material interface.

FIG. 6.

(Color online) Illustration of displacement fields and extracted S-waves of the P-S conversion model with the default parameters. (a) and (b), from the model by XFEM, present the displacement fields along $x$-axis and $y$-axis, respectively. (c) and (d) present the extracted S-waves from the displacements of model by XFEM and FEM, respectively.

FIG. 7.

(Color online) Results of the parametric study presenting the variation of angle of refraction ${\alpha }_t$ and amplitude $A_t$ of transmitted S-waves across an oblique linear interface, in terms of the parameters, including angle of incidence ${\alpha }_i$, modulus $E_{\infty }$ of material 2, frequency $f$, and amplitude $A_i$ of incident P-waves.

FIG. 8.

Illustration of the first snapshot during a period in steady state (100th period) of curl-applied displacement fields ${\mathit{u}}_T$ from the model containing a random-shape inclusion. (a) and (c) correspond to the results of XFEM simulation for the aligned and tilted inclusion, respectively, while (b) and (d) correspond to the results of FEM simulation for the aligned and tilted inclusion, respectively.

FIG. 9.

(Color online) Results of shear modulus $G^{\prime }$ reconstruction from the curl-applied displacement fields of the model containing a random-shape inclusion. (a) and (c) correspond to the results of XFEM simulation for the aligned and tilted inclusion, respectively, while (b) and (d) correspond to the results of FEM simulation for the aligned and tilted inclusion, respectively.

FIG. 10.

(Color online) Illustration of converted S-waves by the P-S conversion XFEM model with the angle of incidence ${\alpha }_i$ = 60 degrees. A central zoom is taken for illustration purpose. (a) corresponds to the model meshed with element size of 2 mm, while (b) corresponds to the model with element size of 1 mm.