Realizing the symmetry-protected Haldane phase in Fermi-Hubbard ladders

Abstract

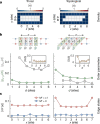
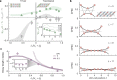
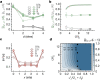
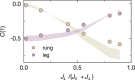
Topology in quantum many-body systems has profoundly changed our understanding of quantum phases of matter. The model that has played an instrumental role in elucidating these effects is the antiferromagnetic spin-1 Haldane chain^1,2. Its ground state is a disordered state, with symmetry-protected fourfold-degenerate edge states due to fractional spin excitations. In the bulk, it is characterized by vanishing two-point spin correlations, gapped excitations and a characteristic non-local order parameter^3,4. More recently it has been understood that the Haldane chain forms a specific example of a more general classification scheme of symmetry-protected topological phases of matter, which is based on ideas connected to quantum information and entanglement^5-7. Here, we realize a finite-temperature version of such a topological Haldane phase with Fermi-Hubbard ladders in an ultracold-atom quantum simulator. We directly reveal both edge and bulk properties of the system through the use of single-site and particle-resolved measurements, as well as non-local correlation functions. Continuously changing the Hubbard interaction strength of the system enables us to investigate the robustness of the phase to charge (density) fluctuations far from the regime of the Heisenberg model, using a novel correlator.

Fig. 1. Probing topological phases in spin-1/2 ladders of cold atoms.

a, Realization of tailored spin-1/2 ladders in a single plane of a 3D optical lattice with a potential shaped by a DMD. The dilute wings of the potential are well separated from the homogeneous ladder systems. Using quantum gas microscopy, we obtain fully spin- and density-resolved images of the system. The inset shows a single-shot fluorescence image of the prepared ladder without spin resolution. b, c, Connecting spin-1/2 ladders to integer-spin chains by grouping pairs of spins in unit cells. For diagonal unit cells (b) the AFM Heisenberg ladder adiabatically connects to the Haldane spin-1 chain showing spin-1/2 edge states and hidden long-range order (that is, AFM order interspersed with S^z = 0 unit cells). For vertical unit cells (c), the system is in the topologically trivial phase dominated by singlets on the rungs, forming a spin-0 chain. We adapt the edges of the system to match the respective unit cell, that is straight edges for vertical unit cells and tilted edges for diagonal unit cells, which we realize by blocking one site on each end. The energy spectra of the systems grouped by total magnetization M^z display gapped fourfold near-degenerate ground states for the topological configuration and a single ground state for the trivial one. Sketch for L = 7.

Fig. 2. Trivial versus topological configurations.

a, The atomic density distribution ⟨$\hat{n}$⟩ of ladders with diagonal and vertical unit cells. b, The amplitudes of the spin-string correlator $g_{S^z,R^z}$ (green circles) and the string-only correlator $g_{\mathbb{𝟙},R^z}$ (grey squares) observed as a function of the spin distance over d unit cells. The cartoon illustrates the unit cells, the total spin S^z per unit cell and the string correlators for a subsystem with d = 3. In the trivial configuration (rung unit cells), $\left|g_{\mathbb{𝟙},R^z}\left(d\right)\right|$ is well above zero, whereas $\left|g_{S^z,R^z}\left(d\right)\right|$ is rapidly vanishing at d > 1. By contrast, for the topological configuration (diagonal unit cells), $\left|g_{S^z,R^z}\left(d\right)\right|$, shows a long-range correlation, whereas $\left|g_{\mathbb{𝟙},R^z}\left(d\right)\right|$ is close to zero. In both cases, the two-point spin–spin correlation C(d) decays rapidly to zero as a function of the distance d (insets). The correlators $g_{\mathbb{𝟙},R^z},g_{S^z,R^z}$ and C(d) are evaluated for fixed total magnetization $m^z$  = 0. c, Amplitudes of the rung- and inversion-averaged local magnetizations $\left|m^z\left(x\right)\right|$ plotted as a function of position x along the chains for different $m^z$. In the unbalanced spin sector of the topological configuration ($m^z$ = ±1), the result displays a localization of the excess spins at the edges, signalling the presence of edge states. All data were taken with $J_{\perp }/J_{\parallel }=1.3\left(2\right)$. Error bars denote one standard error of the mean (s.e.m.) and are smaller than their marker size if not visible. Source data

Fig. 3. Influence of spin-coupling strength on the string order parameters and the edge states.

a, The two string order parameters, $g_{S^z,R^z}$ (green) and $g_{\mathbb{𝟙},R^z}$ (grey), for both trivial (left) and topological (right) configurations measured as a function of $J_{\perp }/(J_{\perp }+J_{\parallel })$. Both $g_{S^z,R^z}$ and $g_{\mathbb{𝟙},R^z}$ stay finite in their respective phases and are largely consistent with zero in the other phase. The data were taken at a chain length of L = 5 except for one data point marked by a triangle at L = 7. Shaded curves are the ED results of the two order parameters at finite entropy per particle, S/N = (0.3−0.45) k_B and L = 5. The inset shows the measured $g_{S^z,R^z}$ as a function of the chain length L at $J_{\perp }/J_{\parallel }=1.3\left(2\right)$ (that is, $J_{\perp }/(J_{\perp }+J_{\parallel })=0.56\left(4\right)$). The decay in the magnitude of the string order parameter with length is expected at finite temperatures in quantitative agreement with ED results (lines) at S/N ≈ 0.4 k_B. b, Edge state localization at $J_{\perp }/J_{\parallel }=1.3\left(2\right)$. In the $m^z$ = ±1 spin sectors of the topological configuration, the unit cell local magnetization $\left|m^z\left(k\right)\right|$ at chain position k shows excess magnetization localized at the edges for different lengths. The black line is a fit to our inversion-averaged data. c, The localization length ξ of the edge states increases with the leg coupling $J_{\parallel }$ but saturates at a value set by temperature and system size L = 5. Lines are ED results at S/N = 0.3 k_B and 0 k_B. The inset shows the independence of ξ with respect to L extracted from the plots in b, as well as ED results for S/N = 0.3 k_B. Error bars denote one standard error of the mean (s.e.m) and are smaller than their marker size if not visible. Source data

Fig. 4. Robustness of the Haldane phase to density fluctuations.

a, b, The hidden SPT order is preserved even at low Hubbard interactions, as revealed by the novel string correlators $\left|{\tilde{g}}_{S^z,P^{\downarrow }}\left(d\right)\right|$ (green circles) and $\left|g_{\mathbb{𝟙},P^{\downarrow }}\left(d\right)\right|$ (grey squares) on the basis of the spin-down parity ${\hat{P}}^{\downarrow }$. $\left|{\tilde{g}}_{S^z,P^{\downarrow }}\right|$ stays non-zero, whereas $\left|g_{\mathbb{𝟙},P^{\downarrow }}\right|$ is consistent with zero for d = L − 1 over the measured interaction range. The same qualitative behaviour is seen in zero-temperature DMRG calculations (shaded line) with $L\to \infty$. c, Spatial distribution of excess magnetization ($m^z$ = ±1) for decreasing $U/t_{\parallel }$. Even far away from the Heisenberg regime, the edge state signal remains strong and only diminishes for very weak $U/t_{\parallel }$. d, Map of zero-temperature DMRG $\left(L\to \infty \right)$ results for the spin-string correlator in the entire parameter space of the topological phase. It shows a strictly non-zero ${\hat{g}}_{S^z,P^{\downarrow }}$ while $g_{\mathbb{𝟙},P^{\downarrow }}\left(L-1\right)=0$ everywhere in this phase. The black circles indicate the parameters of the measurements. All experimental data were taken at $J_{\perp }/J_{\parallel }=1.3\left(2\right)$ and L = 5 in the tilted geometry. $m^z$ = 0 in a, b and d. Error bars denote one standard error of the mean (s.e.m.) and are smaller than their marker size if not visible. Source data

Extended Data Fig. 1. Density engineering.

a, Repulsive light shaped with a DMD splits the system into four independent ladders in the centre surrounded by a low-density bath. The density of the ladders is n = 0.992 with a standard deviation of 0.03. b, The occupation histograms show the normalized occurrence of total atom numbers in each ladder and the normalized occurrence in the surrounding bath for L = 7. Almost 25% of the ladder realizations have N = 2L.

Extended Data Fig. 2. Nearest-neighbour spin correlations.

The nearest-neighbour spin correlation C(1) for different $J_{\perp }/J_{\parallel }$ in the L = 5 system. The brown (purple) points refer to the correlations along the rung (leg). The shaded areas correspond to the correlations in the Heisenberg model with an entropy of S/N = (0.3−0.4) k_B per particle. Both theoretical and experimental values are obtained from the magnetization sector $m^z$ = 0.