Clonal dynamics of haematopoiesis across the human lifespan
- PMID: 35650442
- PMCID: PMC9177428
- DOI: 10.1038/s41586-022-04786-y
Clonal dynamics of haematopoiesis across the human lifespan
Abstract
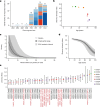
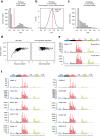
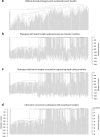
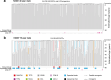
Age-related change in human haematopoiesis causes reduced regenerative capacity1, cytopenias2, immune dysfunction3 and increased risk of blood cancer4-6, but the reason for such abrupt functional decline after 70 years of age remains unclear. Here we sequenced 3,579 genomes from single cell-derived colonies of haematopoietic cells across 10 human subjects from 0 to 81 years of age. Haematopoietic stem cells or multipotent progenitors (HSC/MPPs) accumulated a mean of 17 mutations per year after birth and lost 30 base pairs per year of telomere length. Haematopoiesis in adults less than 65 years of age was massively polyclonal, with high clonal diversity and a stable population of 20,000-200,000 HSC/MPPs contributing evenly to blood production. By contrast, haematopoiesis in individuals aged over 75 showed profoundly decreased clonal diversity. In each of the older subjects, 30-60% of haematopoiesis was accounted for by 12-18 independent clones, each contributing 1-34% of blood production. Most clones had begun their expansion before the subject was 40 years old, but only 22% had known driver mutations. Genome-wide selection analysis estimated that between 1 in 34 and 1 in 12 non-synonymous mutations were drivers, accruing at constant rates throughout life, affecting more genes than identified in blood cancers. Loss of the Y chromosome conferred selective benefits in males. Simulations of haematopoiesis, with constant stem cell population size and constant acquisition of driver mutations conferring moderate fitness benefits, entirely explained the abrupt change in clonal structure in the elderly. Rapidly decreasing clonal diversity is a universal feature of haematopoiesis in aged humans, underpinned by pervasive positive selection acting on many more genes than currently identified.
© 2022. The Author(s).
Conflict of interest statement
D.H.S. has received consultancy fees from Wugen. G.S.V. has received consultancy fees from STRM.BIO and is a remunerated member of AstraZeneca’s Scientific Advisory Board. D.G.K. has received research funding from STRM.BIO.
Figures
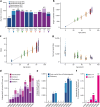
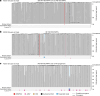
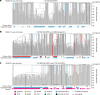
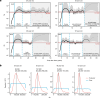









Comment in
-
Blood's life history traced through genomic scars.Nature. 2022 Jun;606(7913):255-256. doi: 10.1038/d41586-022-01304-y. Nature. 2022. PMID: 35650394 No abstract available.
References
-
- Guralnik JM, Eisenstaedt RS, Ferrucci L, Klein HG, Woodman RC. Prevalence of anemia in persons 65 years and older in the United States: evidence for a high rate of unexplained anemia. Blood. 2004;104:2263–2268. - PubMed
-
- Castle SC. Clinical relevance of age-related immune dysfunction. Clin. Infect. Dis. 2000;31:578–585. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

