A semantics, energy-based approach to automate biomodel composition
- PMID: 35657966
- PMCID: PMC9165793
- DOI: 10.1371/journal.pone.0269497
A semantics, energy-based approach to automate biomodel composition
Abstract
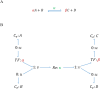
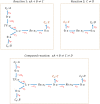
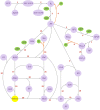
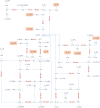
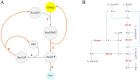
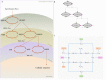
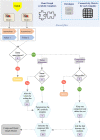
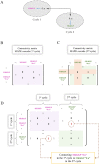
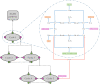
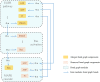
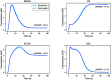
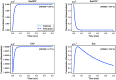
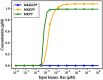
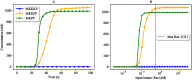
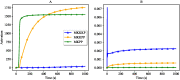
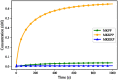
Hierarchical modelling is essential to achieving complex, large-scale models. However, not all modelling schemes support hierarchical composition, and correctly mapping points of connection between models requires comprehensive knowledge of each model's components and assumptions. To address these challenges in integrating biosimulation models, we propose an approach to automatically and confidently compose biosimulation models. The approach uses bond graphs to combine aspects of physical and thermodynamics-based modelling with biological semantics. We improved on existing approaches by using semantic annotations to automate the recognition of common components. The approach is illustrated by coupling a model of the Ras-MAPK cascade to a model of the upstream activation of EGFR. Through this methodology, we aim to assist researchers and modellers in readily having access to more comprehensive biological systems models.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
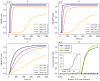
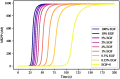
Similar articles
-
SemGen: a tool for semantics-based annotation and composition of biosimulation models.Bioinformatics. 2019 May 1;35(9):1600-1602. doi: 10.1093/bioinformatics/bty829. Bioinformatics. 2019. PMID: 30256901 Free PMC article.
-
Hierarchical semantic composition of biosimulation models using bond graphs.PLoS Comput Biol. 2021 May 13;17(5):e1008859. doi: 10.1371/journal.pcbi.1008859. eCollection 2021 May. PLoS Comput Biol. 2021. PMID: 33983945 Free PMC article.
-
Multiple ontologies in action: composite annotations for biosimulation models.J Biomed Inform. 2011 Feb;44(1):146-54. doi: 10.1016/j.jbi.2010.06.007. Epub 2010 Jun 30. J Biomed Inform. 2011. PMID: 20601121 Free PMC article.
-
The principals of meaning: Extracting semantic dimensions from co-occurrence models of semantics.Psychon Bull Rev. 2016 Dec;23(6):1744-1756. doi: 10.3758/s13423-016-1053-2. Psychon Bull Rev. 2016. PMID: 27138012 Review.
-
Path-based knowledge reasoning with textual semantic information for medical knowledge graph completion.BMC Med Inform Decis Mak. 2021 Nov 29;21(Suppl 9):335. doi: 10.1186/s12911-021-01622-7. BMC Med Inform Decis Mak. 2021. PMID: 34844576 Free PMC article. Review.
Cited by
-
Computational fluid dynamic modeling of the lymphatic system: a review of existing models and future directions.Biomech Model Mechanobiol. 2024 Feb;23(1):3-22. doi: 10.1007/s10237-023-01780-9. Epub 2023 Oct 30. Biomech Model Mechanobiol. 2024. PMID: 37902894 Free PMC article. Review.
References
-
- Le Novere N, Bornstein B, Broicher A, Courtot M, Donizelli M, Dharuri H, et al. BioModels Database: a free, centralized database of curated, published, quantitative kinetic models of biochemical and cellular systems. Nucleic acids research. 2006;34(suppl_1):D689–D691. doi: 10.1093/nar/gkj092 - DOI - PMC - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

