The impact of genetic modifiers on variation in germline mutation rates within and among human populations

Abstract

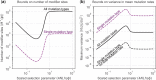
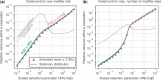
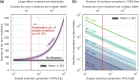
Mutation rates and spectra differ among human populations. Here, we examine whether this variation could be explained by evolution at mutation modifiers. To this end, we consider genetic modifier sites at which mutations, "mutator alleles," increase genome-wide mutation rates and model their evolution under purifying selection due to the additional deleterious mutations that they cause, genetic drift, and demographic processes. We solve the model analytically for a constant population size and characterize how evolution at modifier sites impacts variation in mutation rates within and among populations. We then use simulations to study the effects of modifier sites under a plausible demographic model for Africans and Europeans. When comparing populations that evolve independently, weakly selected modifier sites (2Nes≈1), which evolve slowly, contribute the most to variation in mutation rates. In contrast, when populations recently split from a common ancestral population, strongly selected modifier sites (2Nes≫1), which evolve rapidly, contribute the most to variation between them. Moreover, a modest number of modifier sites (e.g. 10 per mutation type in the standard classification into 96 types) subject to moderate to strong selection (2Nes>1) could account for the variation in mutation rates observed among human populations. If such modifier sites indeed underlie differences among populations, they should also cause variation in mutation rates within populations and their effects should be detectable in pedigree studies.

Keywords: germline mutations; human evolution; modifiers; mutation rate; mutation spectra; mutators; pedigree studies; population genetics.

Fig. 1.

Effect of modifier sites on (a) expected mutation rates and (b) variance of mean mutation rates. We estimate both quantities and their standard error (SE) for each combination of $M$ and the scaled selection parameter $4N\mathit{Lhs}\varphi$ (varying $\varphi$) from simulations (see Simulations). In most cases, the SEs are too small to see and therefore not shown. Analytical results are calculated from Equations (13) and (14). We assume $N=2\mathrm{ }\times {10}^3$ with other parameters chosen to match population-scaled values in humans (see Parameters and Table 1).

Fig. 2.

Upper bound on the number of modifier sites (a) and on variance in mean mutation rates (b), assuming that the expected mutation rate equals the estimated rate in humans. We show both quantities for modifier sites that affect one of 96 mutation types (dashed lines) and for those that affect all mutation types (solid lines). For modifier sites that only affect a single mutation type, we show both their effect on variance at sites they affect and on the total mutation rate. Each quantity was calculated using Equations (16) and (17). We assumed scaled parameter values roughly based on humans with $N=2\mathrm{ }\times {10}^4\mathrm{ }$(see Parameters and Table 1).

Fig. 3.

Summary of parameter ranges where modifier sites generate population specific peaks in mutation rates. For a given $M$ and $\varphi$, we show the probability that (a) a single mutation rate trajectory or (b) sets of 96 trajectories are peak-like, or the probability that (c) the largest enrichment per set is greater than 1.1 (see Tests of variance between populations). (d) A cartoon illustrating how we categorize trajectories based on the number of windows that are above the elevated or peaked thresholds. For individual trajectories (a), we show the probability of being multielevated (interior color). For sets of trajectories (b), we show the expected number of peak-like trajectories in a peak-like set (interior color; null values are colored white). For both (a and b), we show whether most trajectories or sets are not-peaked or multielevated (edge color). For enrichments (c), we show the 95% quantile of enrichment values (interior color). We vary $\varphi$ to span the range of selection parameters and vary $M$ between one and the maximum number of modifier sites possible, $M^{\mathrm{*}}\left(\varphi \right)$ (Equation 16). In Supplementary Figs. 14–17, we show similar results for models that relax some of our simplifying assumptions.

Fig. 4.

Parameter ranges in which both enrichments and peak-like sets occur with probability $\ge 0.01$ under different models and criteria for peak-like trajectories. a) Our basic model. b) A model in which mutation types have different expected rates. c) A model in which mutator alleles are selected on due to their effects on germline and somatic mutation rates. d) A model in which mutator alleles affect multiple mutation types. For all models, we show the parameter ranges for our restrictive (dark grey) and relaxed (light grey) definitions of peak-like trajectories (see Tests of variance in mutation rates between populations and Supplementary Fig. 14 for definitions). See Supplementary Figs. 15–17 for additional details about and more results for each model (akin to Fig. 3). We calculate the maximal number of modifier sites for a given scaled selection parameter (which varies across models) from Equation (16).

Fig. 5.

Variance in mutation rates within a population as a function of the effect size of modifier sites. We show the expected variance within a population (relative to a fixed expected rate, $E\left(V\left(u|q\right)\right)/E^2\left(u\right)$) at steady state arising from: (a) one modifier site and (b) the maximum number of modifier sites conditional on a fixed expected rate (Equation 16). For simulated results with a single site (a), we estimate the average heterozygosity at modifier sites in simulations with $M={10}^3$ (calculated as described in Simulations) and the contribution to variance within a population relying on Equation (11). When assuming the maximum number of modifier sites (b), this estimated contribution and its SE are scaled by $M^{\mathrm{*}}(\varphi )$ (based on Equation (16) and assuming $\widehat{u}=1.25\mathrm{ }\times {10}^{-7}/\mathrm{bp}/\mathrm{gen}$, the estimated human mutation rate scaled for population size). In most cases, the SEs are too small to see. We calculate the analytical predictions from the expected heterozygosity, which is calculated by integrating over the stationary distribution based on Equation (15); we also show the results of the simple approximations described in the text. For comparison, we show the corresponding variance between populations (gray curve) based on Equation (14). Both simulated and analytical results assume$\mathrm{ }N=2\mathrm{ }\times \mathrm{ }{10}^3$ with other parameters chosen to match population-scaled values in humans (see Parameters and Table 1). These results are insensitive to plausible variation in model parameters (Supplementary Fig. 3).

Fig. 6.

Identifying the effects of mutator alleles in a pedigree study of mutation rates. (a) The expected number of de novo mutations (± 1 SD) in trios with and without a mutator. (b) The expected number of mutators sampled (± 1 SD) in a study with 1,500 trios, based on our steady state approximations [Equation (8) and Supplementary Section 6]. The vertical red lines denote the minimum effect size at which we expect a mutator to be detectable (with $P\le 0.05)$. For the purpose of this illustration, we assume a simple null model of mutations in the absence of mutators and ignore potential complications. We further assume that mutators affect all mutations (instead of, e.g. a specific mutation type) and rely on parameter values that are plausible for humans (Table 1) while varying $\varphi$.