Asymmetric host movement reshapes local disease dynamics in metapopulations

Abstract

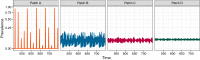
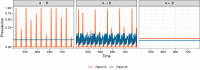
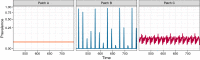
Understanding how the movement of individuals affects disease dynamics is critical to accurately predicting and responding to the spread of disease in an increasingly interconnected world. In particular, it is not yet known how movement between patches affects local disease dynamics (e.g., whether pathogen prevalence remains steady or oscillates through time). Considering a set of small, archetypal metapopulations, we find three surprisingly simple patterns emerge in local disease dynamics following the introduction of movement between patches: (1) movement between identical patches with cyclical pathogen prevalence dampens oscillations in the destination while increasing synchrony between patches; (2) when patches differ from one another in the absence of movement, adding movement allows dynamics to propagate between patches, alternatively stabilizing or destabilizing dynamics in the destination based on the dynamics at the origin; and (3) it is easier for movement to induce cyclical dynamics than to induce a steady-state. Considering these archetypal networks (and the patterns they exemplify) as building blocks of larger, more realistically complex metapopulations provides an avenue for novel insights into the role of host movement on disease dynamics. Moreover, this work demonstrates a framework for future predictive modelling of disease spread in real populations.

Figure 1

Connecting multiple patches with the same parameters and initial conditions results in reduced peak pathogen prevalence and dampened oscillations in patches further down the chain. Here, patches are connected such that $A\to B\to C\to D$. Each panel indicates the prevalence (i.e., the proportion of the patch population currently infected with the pathogen) over time in that particular patch. Because all patches have the same parameters and initial conditions (see Methods), all patches would have the same dynamics (i.e., cycles, as seen in) in the absence of movement between patches. Thus, all differences between patch time series are due to immigration from and emigration to other patches in the chain. Note also that completing the circle (such that $A\to B\to C\to D\to A$) would again make all patches identical, removing any distinction between origin and destination patches. Transient dynamics are omitted from the time series for clarity.

Figure 2

Destination patches tend to inherit origin patch dynamics when linking patches with different model parameterizations. Panels correspond to network structure, with line color indicating the prevalence (i.e., the proportion of the patch population currently infected with the pathogen) through time in particular patches. While in isolation (left column), patch A has oscillatory dynamics and patch B has steady-state dynamics (see Methods), when the two patches are linked by movement, the destination patch inherits the dynamics of the origin patch (center and right panels). This is true regardless of the direction of the movement (but does depend on the rate of movement; see Supporting Information Fig. S4). Transient dynamics are omitted from the time series for clarity.

Figure 3

When multiple origin patches differ in their dynamics, the destination patch inherits oscillations over steady-states. As in Fig. 1, panels correspond to individual patches, with lines indicating the prevalence (i.e., the proportion of the patch population currently infected with the pathogen) through time. Here, we have patches A and B feeding into patch C at the same rate; $A\to C\leftarrow B$. A and C are parametrized to produce steady-state dynamics in the absence of movement (see Methods). B shows oscillatory dynamics, with all other parameters the same. Note that, even though the parameters of C would lead to a steady-state in the absence of movement, we see oscillatory dynamics being inherited from B. Transient dynamics are omitted from the time series for clarity.

Figure 4

The proportion of patches exhibiting each dynamical regime in each of 100 random networks per network structure ensemble. Each panel shows stacked bar charts, with networks lined up along the horizontal axis, sorted according to the proportion of patches exhibiting oscillatory dynamics. Each bar is colored according to the equilibrium dynamical regime of each of the 25 patches per network. “Extinct” indicates a disease-free equilibrium for that patch, “Stable” indicates a constant prevalence through time, and “Cycles or Chaos” indicates that the prevalence fluctuates through time. “Unconverged” indicates patch dynamics that could not be classified within the timescale of the simulation. For example, looking at the tree networks, every patch in the left-most network exhibited oscillatory dynamics, while the right most network had 18 ($\approx 75\%$) patches exhibiting “Stable” dynamics. Networks were generated according to one of five algorithms (see Methods). Similar results are obtained with alternative parameter values (Supporting Information Fig. S9).

Figure 5

Triad counts for two of the possible configurations of three-node directed subgraphs in each random metapopulation network that correspond to the aforementioned archetypal networks. Points are grouped according to network structure ensemble (see Methods and top row of Fig. 4). As in Fig. 4, we see that for the “in-star” triad ($A\to C\leftarrow B$), random, modular, and small-world networks tend to have similar values, while tree and scale-free networks differ. In contrast, we see no consistency between differences in the number of chain triads ($A\to B\to C$) and the distribution of patch dynamics.