A Fast Convergent Ordered-Subsets Algorithm With Subiteration-Dependent Preconditioners for PET Image Reconstruction
- PMID: 35679379
- PMCID: PMC9810102
- DOI: 10.1109/TMI.2022.3181813
A Fast Convergent Ordered-Subsets Algorithm With Subiteration-Dependent Preconditioners for PET Image Reconstruction
Abstract
We investigated the imaging performance of a fast convergent ordered-subsets algorithm with subiteration-dependent preconditioners (SDPs) for positron emission tomography (PET) image reconstruction. In particular, we considered the use of SDP with the block sequential regularized expectation maximization (BSREM) approach with the relative difference prior (RDP) regularizer due to its prior clinical adaptation by vendors. Because the RDP regularization promotes smoothness in the reconstructed image, the directions of the gradients in smooth areas more accurately point toward the objective function's minimizer than those in variable areas. Motivated by this observation, two SDPs have been designed to increase iteration step-sizes in the smooth areas and reduce iteration step-sizes in the variable areas relative to a conventional expectation maximization preconditioner. The momentum technique used for convergence acceleration can be viewed as a special case of SDP. We have proved the global convergence of SDP-BSREM algorithms by assuming certain characteristics of the preconditioner. By means of numerical experiments using both simulated and clinical PET data, we have shown that the SDP-BSREM algorithms substantially improve the convergence rate, as compared to conventional BSREM and a vendor's implementation as Q.Clear. Specifically, SDP-BSREM algorithms converge 35%-50% faster in reaching the same objective function value than conventional BSREM and commercial Q.Clear algorithms. Moreover, we showed in phantoms with hot, cold and background regions that the SDP-BSREM algorithms approached the values of a highly converged reference image faster than conventional BSREM and commercial Q.Clear algorithms.
Figures
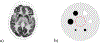

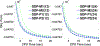
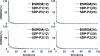





References
-
- Shepp LA and Vardi Y, “Maximum likelihood reconstruction for emission tomography,” IEEE Trans. Med. Imag, vol. 1, no. 2, pp. 113–122, Oct. 1982. - PubMed
-
- Lange K and Carson R, “EM reconstruction algorithms for emission and transmission tomography,” J. Comput. Assist. Tomogr, vol. 8, no. 2, pp. 306–316, 1984. - PubMed
-
- Ahn S, Ross SG, Asma E, Miao J, Jin X, Lishui Cheng SDW, and Manjeshwar1 RM, “Quantitative comparison of OSEM and penalized likelihood image reconstruction using relative difference penalties for clinical PET,” Phys. Med. Biol, vol. 60, no. 15, pp. 5733–5751, 2015. - PubMed
-
- Hudson HM and Larkin RS, “Accelerated image reconstruction using ordered subsets of projection data,” IEEE Trans. Med. Imag, vol. 13, no. 4, pp. 601–609, Dec. 1994. - PubMed
-
- Browne J and De Pierro AR, “A row-action alternative to the EM algorithm for maximizing likelihood in emission tomography,” IEEE Trans. Med. Imag, vol. 15, no. 5, pp. 687–699, Oct. 1996. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Research Materials

