Natural Rubber Blend Optimization via Data-Driven Modeling: The Implementation for Reverse Engineering

Abstract

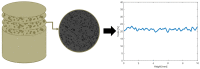
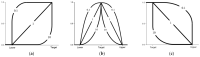
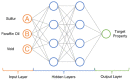
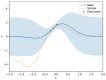
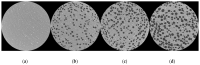
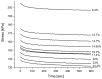
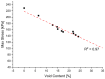
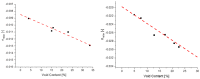
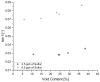
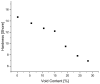
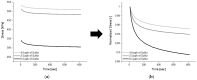
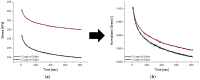
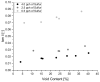
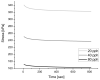
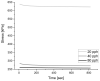
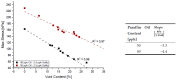
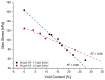
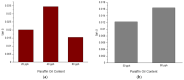
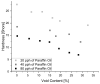
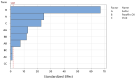
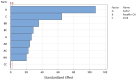
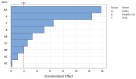
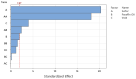
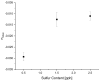
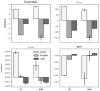
Natural rubber formulation methodologies implemented within industry primarily implicate a high dependence on the formulator's experience as it involves an educated guess-and-check process. The formulator must leverage their experience to ensure that the number of iterations to the final blend composition is minimized. The study presented in this paper includes the implementation of blend formulation methodology that targets material properties relevant to the application in which the product will be used by incorporating predictive models, including linear regression, response surface method (RSM), artificial neural networks (ANNs), and Gaussian process regression (GPR). Training of such models requires data, which is equal to financial resources in industry. To ensure minimum experimental effort, the dataset is kept small, and the model complexity is kept simple, and as a proof of concept, the predictive models are used to reverse engineer a current material used in the footwear industry based on target viscoelastic properties (relaxation behavior, tanδ, and hardness), which all depend on the amount of crosslinker, plasticizer, and the quantity of voids used to create the lightweight high-performance material. RSM, ANN, and GPR result in prediction accuracy of 90%, 97%, and 100%, respectively. It is evident that the testing accuracy increases with algorithm complexity; therefore, these methodologies provide a wide range of tools capable of predicting compound formulation based on specified target properties, and with a wide range of complexity.

Keywords: formulation; machine learning; modeling; natural rubber; optimization; response surface methodology; reverse engineering; viscoelasticity.

Figure 1

A typical compression curve for a foamed elastomeric material where (I) is the initial region with larger tangent modulus, (II) is the buckling region with the reduced tangent modulus, and (III) is the densification zone.

Figure 2

(a) Lissajous curve of raw natural rubber, a nearly-linearly viscoelastic material, (b) Lissajous curve of standard athletic footwear material, a non-linearly viscoelastic material.

Figure 3

A comparison between a 10% and 30% strain test showcasing the low signal-to-noise ratio for the lower strain-level test.

Figure 4

This shows the raw relaxation curve which can be fit to a power function to quantify the long-term behavior under relaxation.

Figure 5

Depicts the workflow for the MATLAB program for quantifying the quantity of voids present within the sample.

Figure 6

Desirability functions for different goals and how weights influence their respective shapes. (a) Minimize the response, (b) Achieve target value, and (c) Maximize the response.

Figure 7

ANN basic architecture.

Figure 8

An illustration of GPR and how more data increases the predictive capabilities.

Figure 9

(a) $\mathsf{\mu }$CT scan of a sample with 0% voids. (b) $\mathsf{\mu }$CT scan of sample with 11.8% voids. (c) $\mathsf{\mu }$CT scan of sample with 19% voids. (d) $\mathsf{\mu }$CT scan of sample with 32.2% voids.

Figure 10

An overlay of relaxation tests of blend 1 at varying levels of void content mentioned in the text to the right of each curve.

Figure 11

Depiction of the linear relationship between max stress experienced in relaxation testing and void content for blend 1.

Figure 12

The relationship between voids and the rate at which stress decays for blend 9 (left) and 10 (right), characterized by ${\mathrm{n}}_{\mathrm{relax}}$.

Figure 13

The Pearson correlation coefficients for each parameter.

Figure 14

The increasing relationship of void content on tan$\mathsf{\delta }$.

Figure 15

The influence of void content on hardness.

Figure 16

(a) Depicts relaxation curves for blends 7, 8 and 9 while (b) represents the normalized curves.

Figure 17

(a) Depicts relaxation curves for blends 1 and 4 while (b) represents the normalized curve, showing a large similarity in regard to the stress decay behavior.

Figure 18

The influence of sulfur content and void content on tan$\mathsf{\delta }$ for blends 7, 8 and 9.

Figure 19

The influence of sulfur content and void content on hardness.

Figure 20

The influence of paraffin oil content on relaxation behavior of NR blend with 1.5 pph of sulfur.

Figure 21

The influence of paraffin oil content on relaxation behavior of NR blend with 2.5 pph of sulfur.

Figure 22

The influence of paraffin oil content on ${\mathsf{\sigma }}_{\mathrm{relax}}$ of NR blend with 1.5 pph of sulfur.

Figure 23

The influence of paraffin oil content on ${\mathsf{\sigma }}_{\mathrm{relax}}$ of NR blend with 2.5 pph of sulfur.

Figure 24

Plot describing the similarity of unique blends by varying void content.

Figure 25

The influence of paraffin oil content on $\tan \mathsf{\delta }$ for a blend with 1.5 pph (a) and 2.5 pph of sulfur (b).

Figure 26

The influence of paraffin oil content on hardness.

Figure 27

The Pareto Chart of Standardized Effects for durometer reading.

Figure 28

The Pareto Chart of Standardized Effects for ${\mathsf{\sigma }}_{\mathrm{relax}}$.

Figure 29

The Pareto Chart of Standardized Effects for ${\mathrm{n}}_{\mathrm{relax}}$.

Figure 30

The Pareto Chart of Standardized Effects for $\tan \mathsf{\delta }$.

Figure 31

The curved response of sulfur content on ${\mathrm{n}}_{\mathrm{relax}}$, further confirming the results in the Pareto chart.

Figure 32

The parity plots for all four ANN models.

Figure 33

The results from the sensitivity analysis for both the linear regression baseline and the ANNs.

Figure 34

The parity plots describing Predicted vs. Experimental for GPR.