A mechano-sensing mechanism for waving in plant roots
- PMID: 35688922
- PMCID: PMC9187721
- DOI: 10.1038/s41598-022-14093-1
A mechano-sensing mechanism for waving in plant roots
Abstract
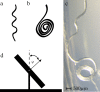
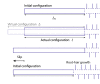
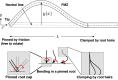
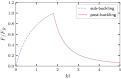
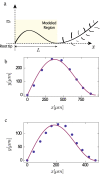
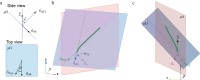
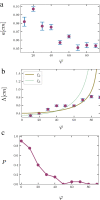
Arabidopsis roots grown on inclined agar surfaces exhibit unusual sinusoidal patterns known as root-waving. The origin of these patterns has been ascribed to both genetic and environmental factors. Here we propose a mechano-sensing model for root-waving, based on a combination of friction induced by gravitropism, the elasticity of the root and the anchoring of the root to the agar by thin hairs, and demonstrate its relevance to previously obtained experimental results. We further test the applicability of this model by performing experiments in which we measure the effect of gradually changing the inclination angles of the agar surfaces on the wavelength and other properties of the growing roots. We find that the observed dynamics is different than the dynamics reported in previous works, but that it can still be explained using the same mechano-sensing considerations. This is supported by the fact that a scaling relation derived from the model describes the observed dependence of the wavelength on the tilt angle for a large range of angles. We also compare the prevalence of waving in different plant species and show that it depends on root thickness as predicted by the model. The results indicate that waving can be explained using mechanics and gravitropism alone and that mechanics may play a greater role in root growth and form than was previously considered.
© 2022. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures
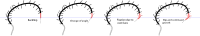

References
-
- Thompson, D. On Growth and Form (1942)
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

