Impact of extra-anatomical bypass on coarctation fluid dynamics using patient-specific lumped parameter and Lattice Boltzmann modeling

Abstract

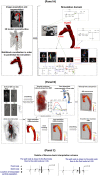
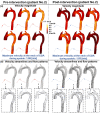
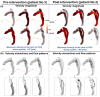
Accurate hemodynamic analysis is not only crucial for successful diagnosis of coarctation of the aorta (COA), but intervention decisions also rely on the hemodynamics assessment in both pre and post intervention states to minimize patient risks. Despite ongoing advances in surgical techniques for COA treatments, the impacts of extra-anatomic bypass grafting, a surgical technique to treat COA, on the aorta are not always benign. Our objective was to investigate the impact of bypass grafting on aortic hemodynamics. We investigated the impact of bypass grafting on aortic hemodynamics using a patient-specific computational-mechanics framework in three patients with COA who underwent bypass grafting. Our results describe that bypass grafting improved some hemodynamic metrics while worsened the others: (1) Doppler pressure gradient improved (decreased) in all patients; (2) Bypass graft did not reduce the flow rate substantially through the COA; (3) Systemic arterial compliance increased in patients #1 and 3 and didn't change (improve) in patient 3; (4) Hypertension got worse in all patients; (5) The flow velocity magnitude improved (reduced) in patient 2 and 3 but did not improve significantly in patient 1; (6) There were elevated velocity magnitude, persistence of vortical flow structure, elevated turbulence characteristics, and elevated wall shear stress at the bypass graft junctions in all patients. We concluded that bypass graft may lead to pseudoaneurysm formation and potential aortic rupture as well as intimal hyperplasia due to the persistent abnormal and irregular aortic hemodynamics in some patients. Moreover, post-intervention, exposures of endothelial cells to high shear stress may lead to arterial remodeling, aneurysm, and rupture.

Figure 1

Reconstructed geometry and simulation domain. Schematic diagram of our developed patient-specific, image-based, computational-mechanics framework that dynamically couples the local hemodynamics with the global circulatory cardiovascular system to investigate the impact of COA and bypass grafting on fluid dynamics in these patients. We used CT images from patients to segment and reconstruct the 3D geometries of the complete aorta. These 3-D geometries were used for investigating hemodynamics using computational fluid dynamics. Local flow dynamics are greatly influenced by upstream and downstream flow conditions that are absent in the flow simulation domain. A lumped-parameter model simulates the function of the left side of the heart. Time-dependent inlet flow at ascending aorta and outlet pressure at descending aorta position were obtained from lumped parameter modeling and applied as boundary conditions. Boundary conditions of the aortic branches were adjusted to match the flow distribution; (b) We compared 4-D flow MRI data and results of our computational framework. The 3-D geometry of the complete aorta was reconstructed using MRI images and the entire volume of Down-sampled LBM data was smoothed (see Four-dimensional flow magnetic resonance imaging (4-D flow MRI section for more details); (c) Modeling complex geometries in LBM. Details of bounce-back interpolation scheme (Here A and E are fluid nodes, B is solid nodes and D represents the location of an interpolated population): (I) The wall-node $\text{C}$ is closer to the fluid-node $\text{A}$ than to the solid-node $\text{B}$ ($\text{q}<1/2$). In this case, interpolations are required to construct post collision state at node D. We constructed the unknown quantities at node A from particles population at node D that will travel to node A after bouncing back off the wall. (II) The wall-node $C$ is closer to the solid-node $B$ than to the fluid-node $A$ ($q\ge 1/2$). In this case, endpoint of propagation state (node D) lies between the boundary node (A) and the wall node (C) and the information of the particle leaving node A and arriving node D will be used to compute the unknown quantities at node A ^,,.

Figure 2

Validation against 4-D flow MRI. (a) We compared 4-D flow MRI data and results of the computational framework (based on lumped parameter model (LPM) and Lattice Boltzmann model (LBM)) in Patients #I to #V. (a) qualitatively (revealed in velocity mapping) and quantitatively by performing Pearson’s product moment correlation analysis on the entire domain at peak systole between smooth down-sampled LBM and 4D flow MRI measurements; (b) qualitatively (revealed in velocity mapping) and quantitatively by performing linear regression and Pearson’s product moment correlation analysis at sample cross sections at peak systole between smooth down-sampled LBM and PC-MRI measurements.

Figure 3

Flow modeling in Patient No. 1 in pre and post intervention status. (a) Time-evolving velocity magnitude at six instances; (b) 3-D (upper row) and 2-D (lower row) streamlines through the aorta at three instances. Baseline characteristics (Patient No. 1): mild-moderate aortic stenosis, mild aortic valve regurgitation, trace mitral regurgitation, COA and hypertension.

Figure 4

Flow modeling in Patient No. 1 in pre and post intervention status. (a) Viscous shear stress (VSS) magnitude; (b) Computed Reynolds Shear stress ($\rho \overline{u^{\prime }{v}^{\prime }},\rho \overline{u^{\prime }{w}^{\prime }}$ and $\rho \overline{w^{\prime }{v}^{\prime }}$) magnitude; (c) Turbulent kinetic energy (TKE), computed as $\frac{1}{2}\rho \left(\overline{u^{\prime 2}}+\overline{v^{\prime 2}}+\overline{w^{\prime 2}}\right)$, where u, v, w and ρ correspond to the three components of the instantaneous velocity vector and density. The bar and prime denote the ensemble averaged and fluctuating components, respectively.

Figure 5

Flow modeling in Patient No. 2 in pre and post intervention status. (a) Time-evolving velocity magnitude at six instances; (b) 3-D (upper row) and 2-D (lower row) streamlines through the aorta at three instances. Baseline characteristics (Patient No. 2): COA and hypertension.

Figure 6

Flow modeling in Patient No. 2 in pre and post intervention status. (a) Viscous shear stress (VSS) magnitude; (b) Computed Reynolds Shear stress ($\rho \overline{u^{\prime }{v}^{\prime }},\rho \overline{u^{\prime }{w}^{\prime }}$ and $\rho \overline{w^{\prime }{v}^{\prime }}$) magnitude; (c) Turbulent kinetic energy (TKE), computed as $\frac{1}{2}\rho \left(\overline{u^{\prime 2}}+\overline{v^{\prime 2}}+\overline{w^{\prime 2}}\right)$, where u, v, w and ρ correspond to the three components of the instantaneous velocity vector and density. The bar and prime denote the ensemble averaged and fluctuating components, respectively.

Figure 7

Flow modeling in Patient No. 3 in pre and post intervention status. (a) Time-evolving velocity magnitude at six instances; (b) 3-D (upper row) and 2-D (lower row) streamlines through the aorta at three instances. Baseline characteristics (Patient No. 1): moderate aortic stenosis, mild mitral regurgitation, severe COA, descending aorta aneurysm, and hypertension.

Figure 8

Flow modeling in Patient No. 3 in pre and post intervention status. (a) Viscous shear stress (VSS) magnitude; (b) Computed Reynolds Shear stress ($\rho \overline{u^{\prime }{v}^{\prime }},\rho \overline{u^{\prime }{w}^{\prime }}$ and $\rho \overline{w^{\prime }{v}^{\prime }}$) magnitude; (c) Turbulent kinetic energy (TKE), computed as $\frac{1}{2}\rho \left(\overline{u^{\prime 2}}+\overline{v^{\prime 2}}+\overline{w^{\prime 2}}\right)$, where u, v, w and ρ correspond to the three components of the instantaneous velocity vector and density. The bar and prime denote the ensemble averaged and fluctuating components, respectively.

Figure 9

Flow modeling in Patients No. 1, 2 and 3 in pre and post intervention status. (a) Wall shear stress in patient #1; (b) Wall shear stress in patient #2; (c) Wall shear stress in patient #3. Blue circles indicate maximum wall shear stress locations.