A Flexible Bayesian Parametric Proportional Hazard Model: Simulation and Applications to Right-Censored Healthcare Data
- PMID: 35693888
- PMCID: PMC9184216
- DOI: 10.1155/2022/2051642
A Flexible Bayesian Parametric Proportional Hazard Model: Simulation and Applications to Right-Censored Healthcare Data
Abstract
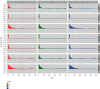
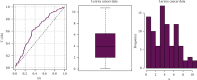
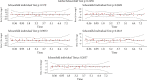
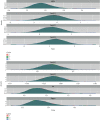
Survival analysis is a collection of statistical techniques which examine the time it takes for an event to occur, and it is one of the most important fields in biomedical sciences and other variety of scientific disciplines. Furthermore, the computational rapid advancements in recent decades have advocated the application of Bayesian techniques in this field, giving a powerful and flexible alternative to the classical inference. The aim of this study is to consider the Bayesian inference for the generalized log-logistic proportional hazard model with applications to right-censored healthcare data sets. We assume an independent gamma prior for the baseline hazard parameters and a normal prior is placed on the regression coefficients. We then obtain the exact form of the joint posterior distribution of the regression coefficients and distributional parameters. The Bayesian estimates of the parameters of the proposed model are obtained using the Markov chain Monte Carlo (McMC) simulation technique. All computations are performed in Bayesian analysis using Gibbs sampling (BUGS) syntax that can be run with Just Another Gibbs Sampling (JAGS) from the R software. A detailed simulation study was used to assess the performance of the proposed parametric proportional hazard model. Two real-survival data problems in the healthcare are analyzed for illustration of the proposed model and for model comparison. Furthermore, the convergence diagnostic tests are presented and analyzed. Finally, our research found that the proposed parametric proportional hazard model performs well and could be beneficial in analyzing various types of survival data.
Copyright © 2022 Abdisalam Hassan Muse et al.
Conflict of interest statement
The authors declare that they have no conflicts of interest.
Figures

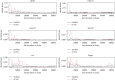
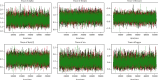
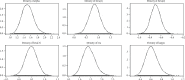
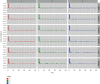
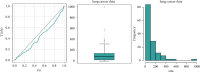
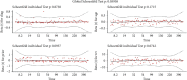

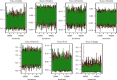

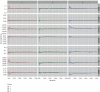

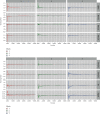
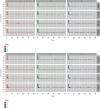
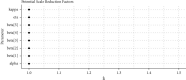
References
-
- Mohamed R. M. K., Shahin O. R., Hamed N. O., Zahran H. Y., Abdellattif M. H. Analyzing the patient behavior for improving the medical treatment using smart healthcare and IoT-based deep belief network. Journal of Healthcare Engineering . 2022;2022:1–8. doi: 10.1155/2022/6389069.6389069 - DOI - PMC - PubMed
-
- Lee C., Zame W., Yoon J., Van Der Schaar M. Deephit: a deep learning approach to survival analysis with competing risks. Proceedings of the 32nd AAAI Conference on Artificial Intelligence; February 2018; New Orleans, LA, USA.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

