An elastic-net penalized expectile regression with applications

Abstract

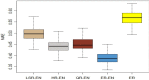
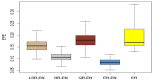
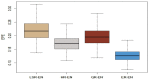
To perform variable selection in expectile regression, we introduce the elastic-net penalty into expectile regression and propose an elastic-net penalized expectile regression (ER-EN) model. We then adopt the semismooth Newton coordinate descent (SNCD) algorithm to solve the proposed ER-EN model in high-dimensional settings. The advantages of ER-EN model are illustrated via extensive Monte Carlo simulations. The numerical results show that the ER-EN model outperforms the elastic-net penalized least squares regression (LSR-EN), the elastic-net penalized Huber regression (HR-EN), the elastic-net penalized quantile regression (QR-EN) and conventional expectile regression (ER) in terms of variable selection and predictive ability, especially for asymmetric distributions. We also apply the ER-EN model to two real-world applications: relative location of CT slices on the axial axis and metabolism of tacrolimus (Tac) drug. Empirical results also demonstrate the superiority of the ER-EN model.

Keywords: 62J05; Expectile regression; SNCD; elastic-net; high-dimensional data; variable selection.

Figure 1.

Boxplots of out-of-sample RMSE for the case of $\epsilon \sim {\chi }^2\left(2\right)$ with p<n.

Figure 2.

Boxplots of out-of-sample MAE for the case of $\epsilon \sim {\chi }^2\left(2\right)$ with p<n.

Figure 3.

Boxplots of out-of-sample EPE for the case of $\epsilon \sim {\chi }^2\left(2\right)$ with p<n.

Figure 4.

Boxplots of out-of-sample RMSE for the case of $\epsilon \sim {\chi }^2\left(2\right)$ with p>n in Situation 1.

Figure 5.

Boxplots of out-of-sample MAE for the case of $\epsilon \sim {\chi }^2\left(2\right)$ with p>n in Situation 1.

Figure 6.

Boxplots of out-of-sample EPE for the case of $\epsilon \sim {\chi }^2\left(2\right)$ with p>n in Situation 1.