A non-parametric Hawkes model of the spread of Ebola in west Africa
- PMID: 35706773
- PMCID: PMC9041724
- DOI: 10.1080/02664763.2020.1825646
A non-parametric Hawkes model of the spread of Ebola in west Africa
Abstract
Recently developed methods for the non-parametric estimation of Hawkes point process models facilitate their application for describing and forecasting the spread of epidemic diseases. We use data from the 2014 Ebola outbreak in West Africa to evaluate how well a simple Hawkes point process model can forecast the spread of Ebola virus in Guinea, Sierra Leone, and Liberia. For comparison, SEIR models that fit previously to the same data are evaluated using identical metrics. To test the predictive power of each of the models, we simulate the ability to make near real-time predictions during an actual outbreak by using the first 75% of the data for estimation and the subsequent 25% of the data for evaluation. Forecasts generated from Hawkes models more accurately describe the spread of Ebola in each of the three countries investigated and result in a 38% reduction in RMSE for weekly case estimation across all countries when compared to SEIR models (total RMSE of 59.8 cases/week using SEIR compared to 37.1 for Hawkes). We demonstrate that the improved fit from Hawkes modeling cannot be attributed to overfitting and evaluate the advantages and disadvantages of Hawkes models in general for forecasting the spread of epidemic diseases.
Keywords: Compartmental models; SEIR models; disease epidemics; non-parametric estimation; point processes; self-exciting.
© 2020 Informa UK Limited, trading as Taylor & Francis Group.
Conflict of interest statement
No potential conflict of interest was reported by the authors.
Figures
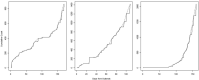

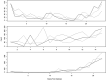

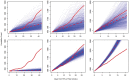

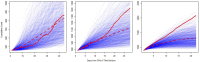
References
-
- Balderama E., Schoenberg F. P., Murray E., and Rundel P. W., Application of branching point process models to the study of invasive red banana plants in Costa Rica, JASA 107 (2012), pp. 467–476. doi: 10.1080/01621459.2011.641402 - DOI
-
- Cao Y., Gillespie D.T., and Petzold L.R., Adaptive explicit-implicit tau-leaping method with automatic tau selection, J. Chem. Phys. 126 (2010), pp. 224101. - PubMed
LinkOut - more resources
Full Text Sources
