On the choice of timescale for other cause mortality in a competing risk setting using flexible parametric survival models

Abstract

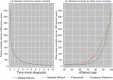
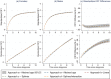
In competing risks settings where the events are death due to cancer and death due to other causes, it is common practice to use time since diagnosis as the timescale for all competing events. However, attained age has been proposed as a more natural choice of timescale for modeling other cause mortality. We examine the choice of using time since diagnosis versus attained age as the timescale when modeling other cause mortality, assuming that the hazard rate is a function of attained age, and how this choice can influence the cumulative incidence functions ( $CIF$ s) derived using flexible parametric survival models. An initial analysis on the colon cancer data from the population-based Swedish Cancer Register indicates such an influence. A simulation study is conducted in order to assess the impact of the choice of timescale for other cause mortality on the bias of the estimated $CIFs$ and how different factors may influence the bias. We also use regression standardization methods in order to obtain marginal $CIF$ estimates. Using time since diagnosis as the timescale for all competing events leads to a low degree of bias in $CIF$ for cancer mortality ( $CI{F}_1$ ) under all approaches. It also leads to a low degree of bias in $CIF$ for other cause mortality ( $CI{F}_2$ ), provided that the effect of age at diagnosis is included in the model with sufficient flexibility, with higher bias under scenarios where a covariate has a time-varying effect on the hazard rate for other cause mortality on the attained age scale.

Keywords: attained age; choice of timescale; competing risks; flexible parametric models; simulation study.

FIGURE 1

Estimated other cause mortality rate, $CI{F}_1$ for death due to cancer and $CI{F}_2$ for other cause mortality for females Note: The estimated other cause mortality rate is given on the time since diagnosis scale (a) and attained age scale (b) for Approaches a—Attained age and d—Splines/Int. a ₀ stands for the age at diagnosis, $CI{F}_1$ for death due to cancer (c,d) and $CI{F}_2$ for other cause mortality (e,f) up to 10 years after diagnosis for ages at diagnosis 70 and 80 for females as estimated by the alternative parametric approaches (Approaches a—Attained age, b—Linear, c—Splines, and d—Splines/Int and the semiparametric different timescales approach)

FIGURE 2

Scenarios of baseline hazards for cancer and other cause mortality Note: (a) Baseline hazard for cancer mortality as a mixture of Weibull distributions and (b) different baseline hazard distributions for other cause mortality

FIGURE 3

Diagram of scenario structure in the simulation Note: PH stands for proportional hazards for gender (non‐PH for non‐proportional hazards). a ₀ stands for the age at diagnosis. The scenarios are numbered from 1 to 24

FIGURE 4

Nested loop line plot of bias in $CI{F}_2(t)$ from each approach over the scenarios Note: The bias of the different approaches is given for ages at diagnosis (60,70,80) and times since diagnosis (1,5,10). Order from outer to inner loops: proportional/nonproportional hazards of gender on attained age (2 levels); standard deviation of age at diagnosis (2 levels, increasing); shape of baseline hazard for other cause mortality (3 levels). The periodic turn of the loops is illustrated by the black lines at the bottom of each plot

FIGURE 5

Standardized $CIF$s for cancer ($CI{F}_1$) and other causes ($CI{F}_2$) Note: (a) Females, (b) males. Panel (c) shows the difference in standardized $CIF$s (Males – Females)