Uniaxial polarization analysis of bulk ferromagnets: theory and first experimental results

Abstract

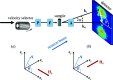
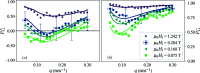
On the basis of Brown's static equations of micromagnetics, the uniaxial polarization of the scattered neutron beam of a bulk magnetic material is computed. The approach considers a Hamiltonian that takes into account the isotropic exchange interaction, the antisymmetric Dzyaloshinskii-Moriya interaction, magnetic anisotropy, the dipole-dipole interaction and the effect of an applied magnetic field. In the high-field limit, the solutions for the magnetization Fourier components are used to obtain closed-form results for the spin-polarized small-angle neutron scattering (SANS) cross sections and the ensuing polarization. The theoretical expressions are compared with experimental data on a soft magnetic nanocrystalline alloy. The micromagnetic SANS theory provides a general framework for polarized real-space neutron methods, and it may open up a new avenue for magnetic neutron data analysis on magnetic microstructures.

Keywords: magnetic nanocomposites; micromagnetics; polarized neutron scattering; small-angle neutron scattering; uniaxial polarization analysis.

Figure 1

Sketch of the SANS setup and of the two most often employed scattering geometries in magnetic SANS experiments. (a) Applied magnetic field perpendicular to the incident neutron beam ( ); (b) . The momentum-transfer or scattering vector corresponds to the difference between the wavevectors of the incident ( ) and the scattered ( ) neutrons, i.e. . Its magnitude for elastic scattering, , depends on the mean wavelength λ of the neutrons and on the scattering angle . For a given λ, sample-to-detector distance and distance from the centre of the direct beam to a certain pixel element on the detector, the q value can be obtained using . The symbols ‘P’, ‘F’ and ‘A’ denote, respectively, the polarizer, spin flipper and analyzer, which are optional neutron optical devices. Note that a second flipper after the sample has been omitted here. In spin-resolved SANS (POLARIS) using a ³He spin filter, the transmission (polarization) direction of the analyzer can be switched by 180° by means of a radiofrequency pulse. SANS is usually implemented as elastic scattering ( ), and the component of along the incident neutron beam [i.e. in (a) and in (b)] is neglected. The angle θ may be conveniently used in order to describe the angular anisotropy of the recorded scattering pattern on a two-dimensional position-sensitive detector. Image taken from Michels (2021 ▸), reproduced by permission of Oxford University Press.

Figure 2

Plot of (upper row) and (lower row) in the saturated state for different values of α (see insets) [equations (60a) and (60b)].

Figure 3

Plot of and (see inset) in the saturated state as a function of α [equations (62a) and (62b)].

Figure 4

Black circles: experimental ratio of nuclear to magnetic scattering of the two-phase alloy NANOPERM (Michels et al., 2012 ▸) ( ; ; log–log plot). Solid line: power-law fit to parametrize the experimental data [equation (63)]. The fit has been restricted to the interval 0.03 < q < 0.3 nm⁻¹, but the fit function is displayed for 0.01 < q < 1.0 nm⁻¹.

Figure 5

Plot of (solid line) and (dashed line) of NANOPERM using equations (62a) and (62b) with given by equation (63) and 0.03 < q < 0.3 nm⁻¹.

Figure 6

Qualitative comparison between experiment and theory. (a)–(d) Two-dimensional experimental polarization of the scattered neutrons of NANOPERM [(Fe_0.985Co_0.015)₉₀Zr₇B₃] at a series of applied magnetic fields (see insets). is horizontal in the plane. The range of momentum transfers is restricted to . (e)–(h) Prediction by the analytical micromagnetic theory (no free parameters) using the experimental ratio [equation (63)] and the structural ( ) and magnetic ( ) interaction parameters of NANOPERM [see text, Michels et al. (2012 ▸) and Honecker et al. (2013 ▸)]. The central white octagons mark the position of the beamstop.

Figure 7

Similar to Fig. 6 ▸, but for .

Figure 8

(Data points) Experimental polarizations (a) and (b) of the scattered neutrons of NANOPERM [(Fe_0.985Co_0.015)₉₀Zr₇B₃] at a series of internal magnetic fields (see inset). For clarity of presentation, error bars are only shown for one field. (Solid lines) Prediction by the analytical micromagnetic theory [equations (44a) and (44b)] using the ratio [equation (63)]. Note the different scales on the ordinates in (a) and (b).

Figure 9

Resulting best-fit values for the correlation lengths and (see inset). Lines are a guide to the eye.

Figure 10

Plot of (upper row) and (lower row) for different applied magnetic fields (see insets). [equation (63)], , .

Figure 11

azimuthally averaged (a) and (b) of the data shown in Fig. 10 ▸.

Figure 12

Plot of (upper row) and (lower row) for different ratios of (see insets). [equation (63)], , .

Figure 13

Plot of (upper row) and (lower row) for different values of (see insets). , , .

Figure 14

Effect of the DMI. Plot of (upper row) and (lower row) as a function of (see insets). [equation (63)], , .

Figure 15

Results for the azimuthally averaged using the sphere form factor (instead of Lorentzian-squared functions) for both and . (a) Field dependence (see inset) of for and . (b) at , , but for increasing (see inset). (c) at , , but for increasing (see inset). [equation (63)], , .