Improving multilevel regression and poststratification with structured priors
- PMID: 35719315
- PMCID: PMC9203002
- DOI: 10.1214/20-ba1223
Improving multilevel regression and poststratification with structured priors
Abstract
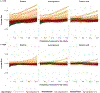
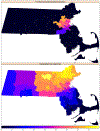
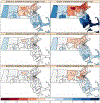
A central theme in the field of survey statistics is estimating population-level quantities through data coming from potentially non-representative samples of the population. Multilevel regression and poststratification (MRP), a model-based approach, is gaining traction against the traditional weighted approach for survey estimates. MRP estimates are susceptible to bias if there is an underlying structure that the methodology does not capture. This work aims to provide a new framework for specifying structured prior distributions that lead to bias reduction in MRP estimates. We use simulation studies to explore the benefit of these prior distributions and demonstrate their efficacy on non-representative US survey data. We show that structured prior distributions offer absolute bias reduction and variance reduction for posterior MRP estimates in a large variety of data regimes.
Keywords: INLA; Multilevel regression and poststratification; Stan; bias reduction; non-representative data; small-area estimation; structured prior distributions.
Figures






















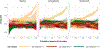















References
-
- Annenberg Center (2008). “The Annenberg Public Policy Center’s National Annenberg Election Survey 2008 Phone Edition (NAES08-Phone) [Data file and code book].” Available from https://www.annenbergpublicpolicycenter.org/tag/data-sets/.
-
- Besag J (1975). “Statistical analysis of non-lattice data.” Journal of the Royal Statistical Society: Series D (The Statistician), 24(3): 179–195.
-
- Bisbee J (2019). “BARP: MRP - Multilevel + BART.” URL https://github.com/jbisbee1/BARP/blob/master/vignettes/BARP.pdf
-
- Chen T and Guestrin C (2016). “Xgboost: A scalable tree boosting system.” In Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 785–794.
Grants and funding
LinkOut - more resources
Full Text Sources
