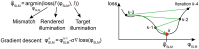Advances in computer-generated holography for targeted neuronal modulation

Abstract

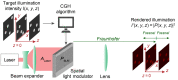
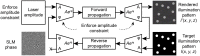
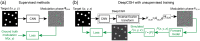
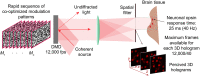
Genetically encoded calcium indicators and optogenetics have revolutionized neuroscience by enabling the detection and modulation of neural activity with single-cell precision using light. To fully leverage the immense potential of these techniques, advanced optical instruments that can place a light on custom ensembles of neurons with a high level of spatial and temporal precision are required. Modern light sculpting techniques that have the capacity to shape a beam of light are preferred because they can precisely target multiple neurons simultaneously and modulate the activity of large ensembles of individual neurons at rates that match natural neuronal dynamics. The most versatile approach, computer-generated holography (CGH), relies on a computer-controlled light modulator placed in the path of a coherent laser beam to synthesize custom three-dimensional (3D) illumination patterns and illuminate neural ensembles on demand. Here, we review recent progress in the development and implementation of fast and spatiotemporally precise CGH techniques that sculpt light in 3D to optically interrogate neural circuit functions.

Keywords: calcium imaging; computer-generated holography; neural modulation; optogenetics; photostimulation; sculpted light.

Fig. 1

Example experimental configuration for CGH. A coherent light source with amplitude $A_{\mathrm{Laser}}(x,y)$, is modulated with an SLM. The shaped beam propagates through an optical system to redistribute light and render a 3D illumination pattern, $I^{\prime }$. The optical system configuration is termed “Fourier holography,” and places the modulator in the pupil plane, at a focal distance, $f$, from a convex lens. The complex field in the image plane, $P(x,y,z=0)$ is determined by applying the Fraunhofer propagation equation [Eq. (2)] to the modulated beam at the SLM, then propagated to other depths, $z$ using the Fresnel wave propagation equation [Eq. (3)]. The rendered illumination, $I^{\prime }$, is given by: $I^{\prime }={|P|}^2$. The CGH algorithm takes as input a target illumination pattern, $I$, in 2D or 3D, and aims to compute the SLM modulation parameters for which the rendered hologram, $I^{\prime }$, best matches $I$.

Fig. 2

Common types of SLMs. (a) LC devices (LC-SLMs) consist of a 2D array of pixel-sized LCs. Their orientation modulates their birefringence and depends on the intensity of the electrical field across each pixel. (b) Continuous DMs consist of a flexible thin mirror that is mechanically deformed by electrical actuators. Segmented DMs eliminate cross-talk between actuators and enable a more precise pixelated modulation. (c) DMDs are MEMS made of miniaturize bistable mirrors. They are binary modulators as each micromirror can be electrically switched between two stable tilt angles.

Fig. 3

GS iterative algorithm for phase-only CGH. A randomly initialized complex field is propagated back and forth between the modulation plane and the image plane. At each step, phase information is retained but the amplitude is updated to either match the illumination profile of the laser in the SLM plane, and the desired intensity distribution, in the image plane. The algorithm typically converges to yield the desired phase modulation at the SLM plane.

Fig. 4

CGH algorithm with iterative nonconvex optimization using gradient descent. CGH computation is formulated as an optimization problem, with an explicit loss function measuring the mismatch between $I$, the desired hologram, and, $I^{\prime }$, the one obtained by applying the phase modulation $\varphi$ on the SLM. The solution to the optimization problem, a phase modulation that minimizes the mismatch, is approximated using gradient descent optimization. Since the optimization problem is not convex, the algorithm may converge to a local minimum. In practice, this algorithm identifies better solutions than iterative GS methods, yet at the expense of further increasing the computation time.

Fig. 5

Customization of the loss function in CGH computation. (a) Hypothetical 3D distribution of a population of optogenetically encoded neurons. The objective is to stimulate a custom ensemble of neurons (labeled in white) while avoiding other neurons also expressing the opsin (labeled in orange). (b) CGH solution with a spatially uniform loss function. (c) CGH solution with a modified loss function that heavily penalizes the presence of light on nontargeted (orange) neurons.

Fig. 6

Deep learning-based CGH computation. (a) CNNs trained to take a target illumination pattern $I(x,y,z)$ as input, can estimate, without iterations, a suitable modulation pattern for the SLM. The parameters of the CNN are optimized by comparing the output of the CNN with ground truth modulation patterns, calculated using another CGH technique or by direct simulation. The mismatch between estimated patterns M and ground truth is measured with a loss function. Supervised learning repeats the operation (green paths) on a large training dataset until the CNN accurately estimates holograms for training samples. (b) DeepCGH with unsupervised training. The hologram that results from the estimated modulation pattern is simulated with a forward model, and the mismatch between the simulated solution, $I^{\prime }(x,y,z)$ and the target, $I(x,y,z)$, provides training feedback. This implementation of DeepCGH is shown for phase SLMs but the method naturally expands to other types of SLMs.

Fig. 7

(a) Accuracy, a measure of mismatch between $I(x,y,z)$ and $I^{\prime }(x,y,z)$, of 1000 random rendered holograms is shown as a function of the computation time for iterative CGH techniques and DeepCGH. DeepCGH solutions have significantly higher accuracy with computation time that is orders of magnitude faster than iterative techniques. CNN1 and CNN2 compare two distinct CNN model sizes and show that increasing the model size can improve the accuracy of renderings, though at the expense of extended computation time. (b) Experimental results in a two-photon holographic microscope compare the two-photon absorption induced in a fluorescent calibration slide with holograms of identical target distribution computed with different CGH algorithms and the computation time for each CGH solution. All three holograms are recorded with the same amount of laser intensity intercepting the slide.

Fig. 8

(a) Optical configuration of 3D-MAP. A collimated Laser beam is projected to the surface of a digital micromirror device to be shaped spatially while a pair of galvomirrors synchronously controls the illumination direction of the incoming wave. (b) Example 3D illumination distribution obtained with 10, rapidly superimposed frames with a revolving oblique illumination.

Fig. 9

Dynamic CGH relies on an algorithm to jointly optimize a set of modulation patterns $M_1(x,y)\dots M_n(x,y)$ so that the renderings resulting from these patterns, $I_{M_1}(x,y)\dots I_{M_n}(x,y)$, accumulate to a time-averaged rendered illumination that best matches the user-specified target illumination distribution. The co-optimized modulation patterns are rapidly displayed on a high-speed SLM (e.g., digital micromirror device). As long as the receptor has a significantly slower response to light, the distribution it perceives corresponds to the time-averaged sum of the coherent holograms successively rendered in the sequence.

Fig. 10

Dynamic CGH can be implemented with inexpensive hardware in a compact format. In the proposed configuration, the DMD modulates a collimated laser beam with a sequence of binary amplitude patterns that are computed by the Dynamic CGH algorithm. A spatial filter eliminates undiffracted light, secondary diffracted orders, and symmetrical copies of the rendered image. The holograms are synthesized in the remaining accessible window and can be used to render images in a human eye, or to stimulate 3D neural circuits in the brain with optogenetics, by taking advantage of the response speed of opsins, which is far slower than the refresh rate of the DMD.