Cortical Motion Perception Emerges from Dimensionality Reduction with Evolved Spike-Timing-Dependent Plasticity Rules

Abstract

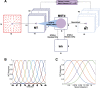
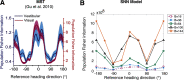
The nervous system is under tight energy constraints and must represent information efficiently. This is particularly relevant in the dorsal part of the medial superior temporal area (MSTd) in primates where neurons encode complex motion patterns to support a variety of behaviors. A sparse decomposition model based on a dimensionality reduction principle known as non-negative matrix factorization (NMF) was previously shown to account for a wide range of monkey MSTd visual response properties. This model resulted in sparse, parts-based representations that could be regarded as basis flow fields, a linear superposition of which accurately reconstructed the input stimuli. This model provided evidence that the seemingly complex response properties of MSTd may be a by-product of MSTd neurons performing dimensionality reduction on their input. However, an open question is how a neural circuit could carry out this function. In the current study, we propose a spiking neural network (SNN) model of MSTd based on evolved spike-timing-dependent plasticity and homeostatic synaptic scaling (STDP-H) learning rules. We demonstrate that the SNN model learns compressed and efficient representations of the input patterns similar to the patterns that emerge from NMF, resulting in MSTd-like receptive fields observed in monkeys. This SNN model suggests that STDP-H observed in the nervous system may be performing a similar function as NMF with sparsity constraints, which provides a test bed for mechanistic theories of how MSTd may efficiently encode complex patterns of visual motion to support robust self-motion perception.SIGNIFICANCE STATEMENT The brain may use dimensionality reduction and sparse coding to efficiently represent stimuli under metabolic constraints. Neurons in monkey area MSTd respond to complex optic flow patterns resulting from self-motion. We developed a spiking neural network model that showed MSTd-like response properties can emerge from evolving spike-timing-dependent plasticity with STDP-H parameters of the connections between then middle temporal area and MSTd. Simulated MSTd neurons formed a sparse, reduced population code capable of encoding perceptual variables important for self-motion perception. This model demonstrates that complex neuronal responses observed in MSTd may emerge from efficient coding and suggests that neurobiological plasticity, like STDP-H, may contribute to reducing the dimensions of input stimuli and allowing spiking neurons to learn sparse representations.

Keywords: MSTd; dimensionality reduction; optic flow; sparse coding; spiking neural network; visual motion processing.

Figure 1.

Model design. A, Architecture of the SNN model. Optic flow stimulus was first processed by an array of MT neurons tuned to speed and direction of motion. The MT activity was converted to Poisson spike trains as the input to the network. The MT neuron group was connected to the MSTd group with a Gaussian projection, which allowed the MSTd neurons to receive input from MT neurons that locate in different areas of the visual field and were tuned to different direction and speed. The MSTd group was reciprocally connected to a group of inhibitory neurons, which regulated the activity of the network. All connections in the network were modulated by STDP-H. The MT→MSTd connection weights and the MSTd group activity were used to reconstruct the input. A fitness function measured the network performance based on the reconstruction accuracy, and STDP-H parameters were evolved with EC to optimize the fitness function. B, Direction tuning curves of the simulated MT neurons. C, Speed tuning curves of the simulated MT neurons. The horizontal axis is plotted on a log₂ scale. deg, Degrees; sec, second.

Figure 2.

Schematic drawings of motion patterns the training and validation dataset was sampled from. The first two rows depict motion patterns in the laminar motion space, and the last two rows depict motion patterns in the spiral motion space.

Figure 3.

Stimulus reconstruction. STDP-H performed dimensionality reduction on the input matrix V and decomposed it into two smaller matrices W, the MT→MSTd weights, and H, the MSTd activity. Each column of the input matrix represented an input instance ${\overrightarrow{v}}_i$, which was visualized as the original flow field. In the figure, the MT→MSTd connection weights W were visualized as a group of basis flow fields. The MSTd activation to this particular stimulus, ${\overrightarrow{h}}_i$, was represented as a column in the matrix H, which denoted the degree of activation of the corresponding basis flow field. Darker color in this visualization corresponded to a higher level of activity. Right, The reconstructed input. The correlation score between the original and the reconstruction of this particular input instance was 0.84.

Figure 4.

Illustration of the effect of homeostatic synaptic scaling on an individual neuron. As the synaptic drive (i.e., input synaptic weights) increases, the firing rate of the neuron increases and exceeds the target firing rate. Homeostatic scaling brings the activity down to the target zone by decreasing the input strength. If the synaptic drive is too low, and the activity of the neuron is below the target firing rate, homeostatic scaling raises the input strength and brings the activity of the neuron back into the target firing zone. Synaptic drive is in arbitrary units, and firing rate is normalized. Figure adapted from Turrigiano and Nelson (2004).

Figure 5.

Best-so-far (BSF) fitness curve across 30 generations of evolutionary process for each network configuration. Solid lines denote the mean fitness scores of all individual runs of the network configuration. Shaded area denotes the SD of the fitness scores.

Figure 6.

Evolved STDP parameters. A, Evolved STDP curves visualized by plotting the changes of synaptic weight (Δw) against the time difference between the presynaptic (t_pre) and postsynaptic (t_post) spikes. The blue curves correspond to the LTP component of STDP (Eq. 7), and the yellow curves correspond to the LTD component (Eq. 8). Solid lines denote the mean values calculated from all evolved network instances (10 network instances for B = 16, 5 network instances for $B=\{36,64,100,144\}$), and the shaded areas denote the SD. B, Area over the LTD or LTP component of the STDP curves.

Figure 7.

Sparseness measurements of different configurations of the SNN model. Population sparseness measured how many neurons were activated by any stimulus, and lifetime sparseness measured how many stimuli any given neuron responds to. The level of sparseness increases with the increased number of MSTd neurons in the network.

Figure 8.

MSTd response to spiral flow fields. A, C, E, Plots show the distributions of tuning with arrows spanning the spiral motion space. Each arrow represents one neuron. B, D, F, Histograms show the distributions of tuning by showing the percentage of simulated neurons tuned to each type of motion. A, B, In a population of 57 neurons recorded from the MSTd area, the tuning of MSTd neurons spanned the entire spiral space, with a large proportion of neurons tuned to expanding motions. Reprinted with permission from Graziano et al. (1994). C–F, Analyses of the entire population of simulated MSTd neurons obtained from five separately evolved and trained network instances with the B = 64 configuration. C, D, In a prescreened for expansion subpopulation of the simulated MSTd neurons, a large proportion of simulated neurons were tuned to expanding motions. E, F, In the entire simulated MSTd neuron population, 278 simulated MSTd neurons had significant tuning to spiral stimuli. The preferred spiral directions distributed evenly.

Figure 9.

MSTd response to spiral flow fields ($B=\{16,36,10,144\}$). A, C, E, G, Distribution of spiral tuning of the prescreened population. Similar to the B = 64 configuration as shown in Figure 8D, a large proportion of simulated neurons were tuned to expanding motions. B, D, F, H, Distribution of spiral tuning of the entire population of simulated MSTd neurons obtained in 10 separately evolved and trained network instances with the B = 16 configuration, and five network instances with the $B=\{36,10,144\}$. Similar to the B = 64 configuration as shown in Figure 8F, the preferred spiral directions distributed evenly.

Figure 10.

3D translation and rotation tuning of example MSTd neurons. A, B, Translation and rotation tuning of an example MST neuron recorded under the visual rotation and translation conditions. Reprinted with permission from Takahashi et al. (2007). C, D, Translation and rotation tuning of an example MSTd neuron from a fully evolved and trained SNN model with the B = 64 configuration. Each contour map shows the Lambert cylindrical equal-area projection of the original data (Snyder, 1987).

Figure 11.

Distribution of 3D translation and rotation tuning of MSTd neurons. A–D, Each data point in the scatter plot represents the preferred azimuth and elevation angles of one neuron. The histograms along the sides of the scatter plots show the marginal distributions. The 2D projections of unit-length 3D preferred direction vectors are shown in the radial plots, including the front, side, and top view. Each radial line in these plots represents one neuron. A, B, MST neurons recorded under the visual rotation and translation conditions. Reprinted with permission from Takahashi et al. (2007). C, D, Simulated MSTd neurons from five separately evolved and trained SNN model with the B = 64 configuration.

Figure 12.

Distribution of 3D translation and rotation tuning of simulated MSTd neurons ($B=\{16,36,10,144\}$). A, C, E, G, The rotational heading preferences of all simulated neurons in each network configuration. B, D, F, H, The translational heading preferences. Each data point in the scatter plot represents the preferred azimuth and elevation angles of one simulated neuron. The histograms along the sides of the scatter plots show the marginal distributions.

Figure 13.

A–F, Distribution of the direction of maximal discriminability for neurons recorded in macaque MSTd (A) and simulated MSTd neurons in the SNN models (B–F). Reprinted with permission from Gu et al. (2010). Both the recorded and the simulated neuron populations showed a bimodal distribution with peaks around the forward (0°) and backward (180°) headings.

Figure 14.

A, B, Population Fisher information computed from neurons recorded in macaque MSTd (A) and from simulated MSTd neurons in the SNN models (B). Reprinted with permission from Gu et al. (2010). The error bands in A show 95% confidence intervals derived from a bootstrap procedure.

Figure 15.

Error in predicting FOE (heading) using the activity of a population of 144 MSTd neurons from each configuration of the network mode l. Simulated MSTd neurons from different configurations of the network exhibited similar levels of accuracy in these two tasks. The interquartile range box represents the middle 50% of the values. The line within the box indicates the median. The red data points mark outliers that are 1.5 times bigger than the interquartile range, and the whiskers extend to the most extreme data points that are not considered outliers. deg, Degrees.