Does Social Distancing Matter for Infectious Disease Propagation? An SEIR Model and Gompertz Law Based Cellular Automaton

Abstract

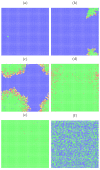
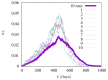
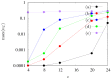
In this paper, we present stochastic synchronous cellular automaton defined on a square lattice. The automaton rules are based on the SEIR (susceptible → exposed → infected → recovered) model with probabilistic parameters gathered from real-world data on human mortality and the characteristics of the SARS-CoV-2 disease. With computer simulations, we show the influence of the radius of the neighborhood on the number of infected and deceased agents in the artificial population. The increase in the radius of the neighborhood favors the spread of the pandemic. However, for a large range of interactions of exposed agents (who neither have symptoms of the disease nor have been diagnosed by appropriate tests), even isolation of infected agents cannot prevent successful disease propagation. This supports aggressive testing against disease as one of the useful strategies to prevent large peaks of infection in the spread of SARS-CoV-2-like diseases.

Keywords: SARS-CoV-2-like disease spreading; compartmental models; computer simulation; epidemy.

Figure 1

Sites in various neighborhoods $\mathcal{N}$ on a square lattice. (a) Von Neumann’s neighborhood ($r=1$, $z=4$); (b) Moore’s neighborhood ($r=\sqrt{2}$, $z=8$); (c) neighborhood with sites up to the third coordination zone ($r=2$, $z=12$); (d) neighborhood with sites up to the fourth coordination zone ($r=\sqrt{5}$, $z=20$); (e) neighborhood with sites up to the fifth coordination zone ($r=2\sqrt{2}$, $z=24$).

Figure 2

Daily death probability $f\left(a\right)$ for patients infected by the coronavirus (SARS-CoV-2, ×, $f_C\left(a\right)$, 50]) and natural death probability (+, $f_G\left(a\right)$, 44]).

Figure 3

Snapshots from direct simulation [52] for $p_{\mathcal{E}}=0.03$, $p_{\mathcal{I}}=0.02$, $R=1$. The assumed ranges of interactions are (a) $r_{\mathcal{E}}=r_{\mathcal{I}}=1$, (b) $r_{\mathcal{E}}=r_{\mathcal{I}}=1.5$, (c) $r_{\mathcal{E}}=r_{\mathcal{I}}=2$, (d,f) $r_{\mathcal{E}}=r_{\mathcal{I}}=2.5$, and (e) $r_{\mathcal{E}}=r_{\mathcal{I}}=3$. The simulation took $t=150$ time steps except for Figure 3f, where the situation after $t>$ 20,000 time steps is presented.

Figure 4

Ten different simulations for values of the neighborhood radius $r_{\mathcal{E}}=r_{\mathcal{I}}$ = 1.5. $p_{\mathcal{E}}=0.03$, $p_{\mathcal{I}}=0.02$.

Figure 5

Dynamics of states fractions for various values of the neighborhood radius $r_{\mathcal{E}}=r_{\mathcal{I}}$. $p_{\mathcal{E}}=p_{\mathcal{I}}=0.005$, $R=10$.

Figure 5

Dynamics of states fractions for various values of the neighborhood radius $r_{\mathcal{E}}=r_{\mathcal{I}}$. $p_{\mathcal{E}}=p_{\mathcal{I}}=0.005$, $R=10$.

Figure 6

Dynamics of states fractions for various values of the neighborhood radius (left) $r_{\mathcal{E}}=r_{\mathcal{I}}$, (middle) $r_{\mathcal{E}}\ge r_{\mathcal{I}}=1$, (right) $3=r_{\mathcal{E}}\ge r_{\mathcal{I}}$. $p_{\mathcal{E}}=0.03$, $p_{\mathcal{I}}=0.02$, $R=10$.

Figure 7

Maximal fraction $n_{\mathcal{I}}$ of agents in state $\mathcal{I}$ as dependent on the number of agents’ neighbours z in the neighborhood. (a) $p_{\mathcal{E}}=p_{\mathcal{I}}=0.005$, $z_E=z_{\mathcal{I}}=z$, (b) $p_{\mathcal{E}}=p_{\mathcal{I}}=0.01$, $z_E=z_{\mathcal{I}}=z$, (c) $p_{\mathcal{E}}=0.03$, $p_{\mathcal{I}}=0.02$, $z_E=z_{\mathcal{I}}=z$, (d) $p_{\mathcal{E}}=0.03$, $p_{\mathcal{I}}=0.02$, $z_E=z$, $z_{\mathcal{I}}=4$, (e) $p_{\mathcal{E}}=0.03$, $p_{\mathcal{I}}=0.02$, $z_E=24$, $z_{\mathcal{I}}=z$.