Optimizing Efficiency and Motility of a Polyvalent Molecular Motor
- PMID: 35744528
- PMCID: PMC9228586
- DOI: 10.3390/mi13060914
Optimizing Efficiency and Motility of a Polyvalent Molecular Motor
Abstract
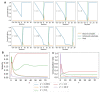
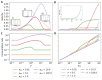
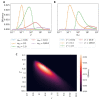
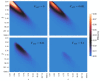
Molecular motors play a vital role in the transport of material within the cell. A family of motors of growing interest are burnt bridge ratchets (BBRs). BBRs rectify spatial fluctuations into directed motion by creating and destroying motor-substrate bonds. It has been shown that the motility of a BBR can be optimized as a function of the system parameters. However, the amount of energy input required to generate such motion and the resulting efficiency has been less well characterized. Here, using a deterministic model, we calculate the efficiency of a particular type of BBR, namely a polyvalent hub interacting with a surface of substrate. We find that there is an optimal burn rate and substrate concentration that leads to optimal efficiency. Additionally, the substrate turnover rate has important implications on motor efficiency. We also consider the effects of force-dependent unbinding on the efficiency and find that under certain conditions the motor works more efficiently when bond breaking is included. Our results provide guidance for how to optimize the efficiency of BBRs.
Keywords: burnt bridge ratchet; computational model; molecular motor.
Conflict of interest statement
The authors declare no conflict of interest.
Figures


Similar articles
-
Substrate stiffness tunes the dynamics of polyvalent rolling motors.Soft Matter. 2021 Feb 19;17(6):1468-1479. doi: 10.1039/d0sm01811b. Soft Matter. 2021. PMID: 33347523
-
Burnt bridge ratchet motor force scales linearly with polyvalency: a computational study.Soft Matter. 2021 Jun 30;17(25):6056-6062. doi: 10.1039/d1sm00676b. Soft Matter. 2021. PMID: 34151336
-
Highly Polyvalent DNA Motors Generate 100+ pN of Force via Autochemophoresis.Nano Lett. 2019 Oct 9;19(10):6977-6986. doi: 10.1021/acs.nanolett.9b02311. Epub 2019 Sep 9. Nano Lett. 2019. PMID: 31402671
-
Protein motors and Maxwell's demons: does mechanochemical transduction involve a thermal ratchet?Adv Biophys. 1990;26:97-134. doi: 10.1016/0065-227x(90)90009-i. Adv Biophys. 1990. PMID: 2150583 Review.
-
Brownian ratchet models of molecular motors.Cell Biochem Biophys. 2003;38(2):191-214. doi: 10.1385/CBB:38:2:191. Cell Biochem Biophys. 2003. PMID: 12777714 Review.
References
-
- Korosec C.S., Forde N.R. The lawnmower: An artificial protein-based burnt-bridge molecular motor. arXiv. 20212109.10293
Grants and funding
LinkOut - more resources
Full Text Sources

